Домашнее задание#

Смоделировать нестационарное обтекание бесконечного цилинда круглого сечения дозвуковым потоком вязкой жидкости методом решётчатого газа Больцмана.

Анимация

Исходные данные:

  • число Рейнольдса \(\mathrm{Re}\);

  • размеры клеточного автомата (число узлов) по горизонтали \(n_x\) и вертикали \(n_y\);

  • скорость потока в единицах решётки \(u_{LB}\);

  • давление газа \(p_\infty\), окружающего расчётную область;

  • плотность окружающего газа \(\rho_\infty\).

Результат моделирования:

  • векторное \(\vec u(x, y)\) и скалярное \(\|\vec u(x, y)\|\) поле скорости;

  • скалярное поле давления газа \(p(x, y)\);

  • скалярное поле плотности газа \(\rho(x, y)\).

Методические указания#

Для решения поставленной задачи полезными являются следующие библиотеки:

import numpy as np
import matplotlib.pyplot as plt
from tqdm import trange

Вспомогательные структуры данных#

Полезно завести вспомогательные структуры данных для хранения начальных условий, результатов и пр.:

# Применение к Python-классу декоратора dataclass
# закономерно приводит к получению дата-класса,
# т.е. класса, предназначенного для хранения данных.
# При этом значительно упрощается описание самого класса.
from dataclasses import dataclass

# frozen=True запрещает изменять значения в экземплярах
@dataclass(frozen=True)
class LBEParams:
    """Хранит исходные данные, необходимые для решателя.
    
    * `Re`: число Рейнольдса.
    * `nx` и `ny`: размеры сетки.
    * `u_lb`: скорость газа в единицах решётки
    * `p_inf`: давление окружающего газа, Па
    * `rho_inf`: плотность газа, кг/м^3
    """
    Re: float = 180.0
    nx: int = 420
    ny: int = 180
    u_lb: float = 0.01
    p_inf: float = 1e5
    rho_inf: float = 1


@dataclass(frozen=True)
class Obstacle:
    """Хранит радиус и координаты центра круга в единицах решётки."""
    radius: float
    cx: float
    cy: float


@dataclass(frozen=True)
class Viscosity:
    """Хранит параметры вязкости газа.
    
    * `nu_lb`: кинематическая вязкость в единицах решётки
    * `k_relax`: коэффициент релаксации
    """
    nu_lb: float
    k_relax: float


# Константы
VELOCITY = np.array([
    [1, 1], [1, 0], [1, -1], [0, 1],
    [0, 0],
    [0, -1], [-1, 1], [-1, 0], [-1, -1]
])
LENCORR = np.array(
    [1/36, 1/9, 1/36, 1/9, 4/9, 1/9, 1/36, 1/9, 1/36]
)
COL_1 = np.array([0, 1, 2])
COL_2 = np.array([3, 4, 5])
COL_3 = np.array([6, 7, 8])

Решатель#

Шаблон кода класса решателя приведён ниже:

class LBESolver:
    def __init__(self, params: LBEParams):
        self.Re = params.Re
        self.nx, self.ny = params.nx, params.ny
        self.u_lb = params.u_lb
        self.p_inf = params.p_inf
        self.rho_inf = params.rho_inf
        # Инициализация доп. переменных
        self._prepare()
    
    def _prepare(self):
        self.ly = self.ny - 1
        self.obs = Obstacle(self.ny // 9, self.nx // 4, self.ny // 2)
        nu_lb = ...
        self.viscosity = Viscosity(nu_lb, ...)
        self.where_obs = np.fromfunction(self._obstacle_fun, (self.nx, self.ny))
        self.v_initial = np.fromfunction(self._init_velo, (2, self.nx, self.ny))
    
    def _obstacle_fun(self, x, y):
        # Определить, какие узлы решётки принадлежат препятствию
        return (x - self.obs.cx)**2 + (y - self.obs.cy)**2 < self.obs.radius**2
    
    def _init_velo(self, d, x, y):
        # Инициализация поля скорости
        return (1 - d)*self.u_lb*(1 + 1e-4*np.sin(2*np.pi * y/self.ly))
    
    def solve(self, iters=100_000, n_steps=100):
        """Основной метод решателя.
        
        * `iters`: количество итераций расчёта
        * `n_steps`: количество раз, которое необходимо сохранить
          данные через равные промежутки времени
        """
        # Для сохранения результатов
        speed_store = []
        p_store = []
        rho_store = []

        fin = self.calc_equilibrium(self.rho_inf, self.v_initial)
        for time in trange(iters):
            # 1. Граничное условие outflow на правой стенке
            #    для населённостей fin
            ...
            # 2. Рассчитать макроскопические величины потока:
            #    давление, плотность, скорость
            rho, u, p = self.calc_macroscopic(fin)
            # 3. Граничное условие inflow на левой стенке
            #    для скорости и плотности
            u[:, 0, :] = ...
            rho[0, :] = ...
            # 4. Расчёт равновесных состояний
            feq = self.calc_equilibrium(rho, u)
            fin[COL_1, 0, :] = ...
            # 5. Фаза столкновения
            fout = ...
            # 6. Условие отражения от преграды
            for i in range(9):
                # Работаем с fout
                ...
            # 7. Фаза распространения (рассмотрите функцию np.roll)
            for i in range(9):
                # Получаем новый fin из fout
                ...
            # 8. Сохранение результатов на некоторых итерациях
            #    (чтобы не занимать слишком много памяти)
            if time % (iters // n_steps) == 0:
                speed_store.append(...) # скорость газа
                p_store.append(...)     # давление
                rho_store.append(...)   # плотность
        
        return speed_store, p_store, rho_store
    
    def calc_macroscopic(self, fin: np.ndarray):
        """Расчёт макроскопических параметров потоков,
        исходя из населённостей (плотностей вероятности) `fin`.
        """
        rho = ...
        u = ...
        p = ...
        return rho, u, p
    
    def calc_equilibrium(self, rho, u):
        """Расчёт равновесного состояния по плотности и скорости газа."""
        feq = ...
        ...
        return feq

Important

Вместо заглушек pass и многоточих ... должна быть ваша реализация кода.

Что и в какой последовательности этот код должен считать?

Рассмотрим блок служебных методов (их имена начинаются с подчёркивания _), вызываемых в конструкторе класса.

Метод _prepare инициализирует дополнительные вспомогательные поля класса. Здесь nu_lb - кинематическая вязкость в единицах решётки. Рассчитывается она через число Рейнольдса \(\mathrm{Re}\), величину характерной скорости потока в единицах решётки \(u_{LB}\) (то, что хранится в LBEParams) и характерный размер геометрии (радиус цилиндра) \(R\):

\[ \nu_{LB} = \cfrac{u_{LB} R}{\mathrm{Re}}. \]

Коэффициент релаксации \(\omega\) (в коде k_relax) является вторым параметром в конструкторе класса Viscosity и считается так:

\[ \omega = \cfrac{1}{3\nu_{LB} + 1/2}. \]

Метод _obstacle_fun достаточно прост: узел принадлежит цилиндру, если его координаты \((x; y)\) лежат внутри окружности, радиус и координаты центра которой известны. В коде эта функция является аргументом для np.fromfunction, в результате работы которой возвращается массив формы (nx, ny) (размер решётки), заполненный булевыми значениями: True, если узел лежит внутри цилиндра, иначе False.

Метод _init_velo аналогично используется в np.fromfunction (получается массив формы (2, nx, ny)). Предназначен для инициализации начальной скорости газа в узлах решётки по формуле

\[ \begin{align}\begin{aligned}\begin{split} \begin{split} u^\text{init}_x(\vec r) &= u_{LB} + \delta u_{LB} = u_{LB} \cdot \left[ 1 + 10^{-4} \cdot \sin\left( \cfrac{2\pi}{n_y - 1} \cdot y \right) \right], \\\end{split}\\u^\text{init}_y(\vec r) &= 0, \end{split} \end{aligned}\end{align} \]

то есть в начальный момент скорость по вертикальной оси распределена неравномерно по всей расчётной области.

Заданная в исходных данных скорость \(u_{LB}\) направлена вдоль оси \(Ox\) слева направо.

Основным методом класса является solve. Что и в какой последовательности он должен делать ясно из комментариев к его коду. С математической точки зрения происходит следующее.

  1. Рассчитывается начальное равновесное состояние. Это нужно для того, чтобы инициализировать массив fin, хранящий все \(f^\text{in}_i(\vec r, t=0)\). В данном случае fin имеет форму (9, nx, ny).

  2. Реализуется граничное условие outflow на правой границе. Входящие в крайний правый слой узлов потоки (индексы COL_3) заменяются на потоки с теми же индексами из предпоследнего слоя (столбца) fin.

  3. Пересчитываются макроскопические параметры потока: \(\rho\), \(\vec u\) и \(p\).

  4. Реализуется граничное условие inflow на левой границе. Оно заключается в том, что на ней всегда скорость \(\vec u\) равна \(\vec u^\text{init} = (u^\text{init}_x; u^\text{init}_y)\). Также на левой границе пересчитывается плотность:

\[ \rho = \cfrac{\rho_2 + 2\rho_3}{1 - u_x}, \]

где \(\rho_2 = f^\text{in}_3 + f^\text{in}_4 + f^\text{in}_5\) и \(\rho_3 = f^\text{in}_6 + f^\text{in}_7 + f^\text{in}_8\).

Обновляется равновесное состояние \(E_i(\rho, \vec u)\) согласно уравнению Максвелла-Больцмана. Считаем соответствующие потоки:

\[\begin{split} \begin{split} f^\text{in}_0 &= E_0(\rho, \vec u) + \left( f^\text{in}_8 - E_8(\rho, \vec u) \right), \\ f^\text{in}_1 &= E_1(\rho, \vec u) + \left( f^\text{in}_7 - E_7(\rho, \vec u) \right), \\ f^\text{in}_2 &= E_2(\rho, \vec u) + \left( f^\text{in}_6 - E_6(\rho, \vec u) \right). \end{split} \end{split}\]

  1. Обновляются входящие извне потоки fin.

  2. Просчитывается фаза столкновения, получаем fout:

\[ f^\text{out}_i(\vec r, t) = f^\text{in}_i(\vec r, t) - \omega \left(f^\text{in}_i(\vec r, t) - E_i(\vec r, \vec u, t) \right). \]

  1. Получаем fin в пристеночных узлах по имеющемуся fout согласно уравнению \(f^\text{in}_i(\vec r, t+\delta t) = f^\text{in}_j(\vec r, t)\) для таких \(i\) и \(j\), что \(\vec v_i = -\vec v_j\). Например, для \(i=2\) имеем \(j=6\).

  2. На фазе распространения необходимо получить для остальных узлов fin из fout:

\[ f^\text{in}_i(\vec r + \vec v_i \delta t, t + \delta t) = f^\text{out}_i(\vec r, t). \]

Что делают методы, вызываемые в методе solve?

Рассмотрим метод calc_macroscopic. Он должен посчитать плотность, скорость и давление газа в ячейках. Делается это для каждого узла по следующим формулам:

\[ \rho(\vec r, t) = \sum\limits_{i=1}^{9} f^\text{in}_i(\vec r, t), \]
\[ \vec u(\vec r, t) = \cfrac{1}{\rho(\vec r, t)} \sum\limits_{i=1}^{9} \vec v_i f^\text{in}_i(\vec r, t), \]
\[ p(\vec r, t) = c_s^2 \rho(\vec r, t). \]

Здесь \(\vec r\) - это радиус-вектор (координаты) узла, \(t\) - текущий момент времени, \(\vec v_i\) - векторы возможных скоростей (\(\vec v_0 = (1; 1)\), \(\vec v_1 = (1; 0)\) и т. д. - см. лекции) - в коде это массив VELOCITY. Скорость звука \(c_s\) на решётке рассчитывается так:

\[ c_s^2 = \cfrac{1}{3}\left( \cfrac{\delta x}{\delta t} \right)^2. \]

Для простоты можно принять \(\delta x / \delta t = 1\), тогда \(c_s^2 = 1/3\).

Перейдём к методу calc_equilibrium. В ней для каждого узла рассчитывается равновесное распределение \(E_i(\rho, \vec u)\):

\[ E_i(\rho, \vec u) = \rho a_i \left( 1 - \cfrac{\vec v_i \cdot \vec u}{c_s^2} + \cfrac{1}{2 c_s^4} (\vec v_i \cdot \vec u)^2 - \cfrac{1}{2 c_s^2}\vec u \cdot \vec u \right). \]

В коде \(a_i\) - это LENCORR.

Моделирование#

Остаётся лишь промоделировать при заданных исходных данных:

# Инициализация исходных данных
params = LBEParams(...)
# Инициализация решателя
solver = LBESolver(params)
# Решение задачи
rho, u, p = solver.solve(...)
# Визуализация
...

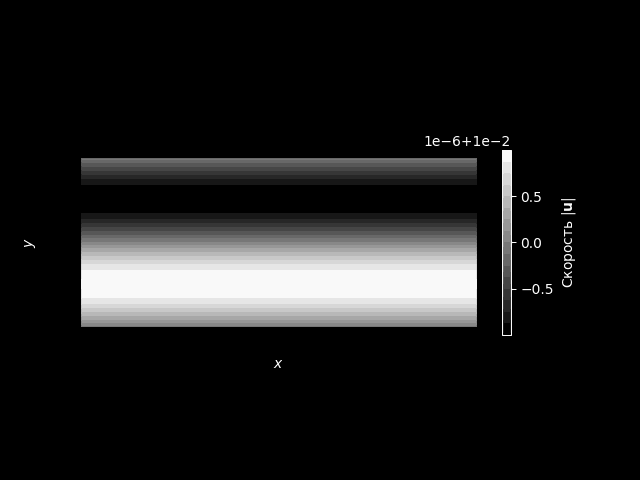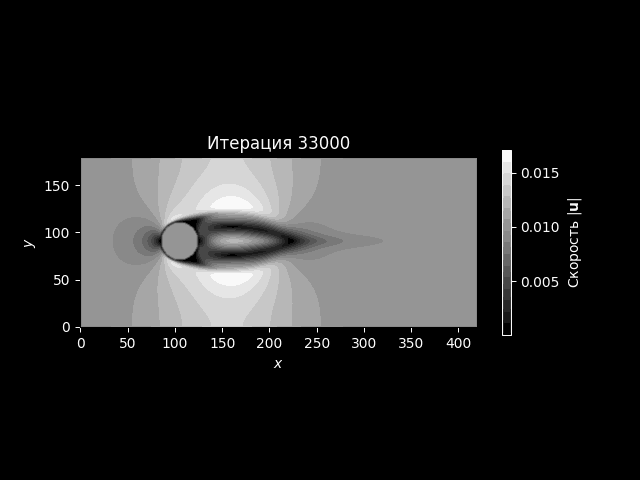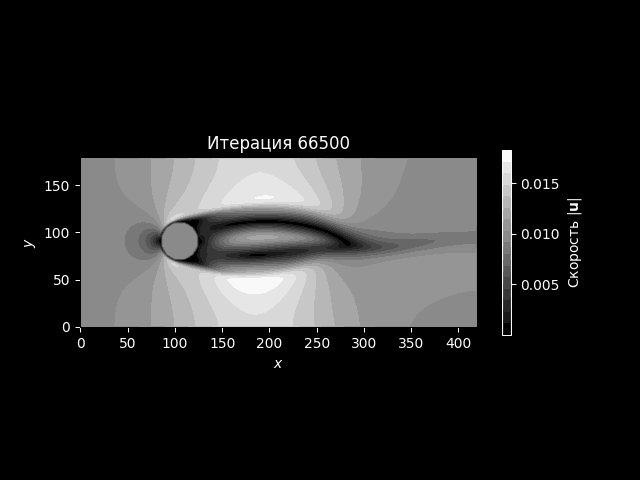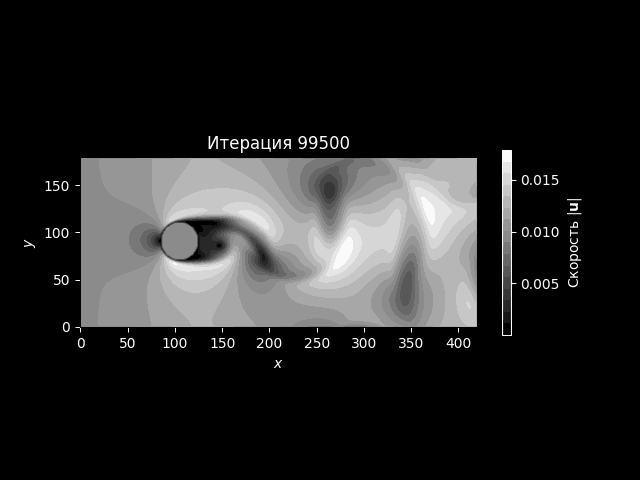
Пример результата#

Пример графика показан на рисунке ниже.

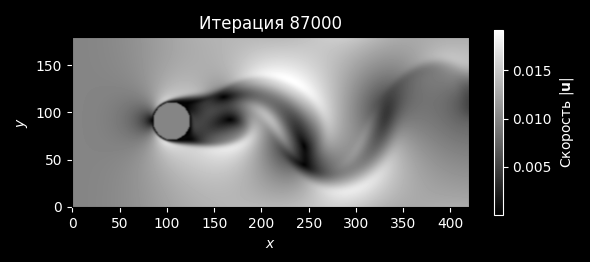
Пример графика

Note

Как сохранять Matplotlib-графики можно узнать здесь.