Лабораторная работа №4. Поиск пути в среде с преградами#

Цель работы - закрепить знания и получить опыт решения задачи поиска кратчайшего пути в дискретном двумерном пространстве с препятствиями.

Описание задачи#

Дано клеточное поле размером \(m \times n\). Шаг между соседними клетками равен 1.

Поле заполнено заданным числом препятствий, расположенных случайным образом. Каждое препятствие имеет ширину в одну клетку и случайную длину в диапазоне длин от \(l_{\rm min}\) до \(l_{\rm max}\) клеток. Длина является случайной величиной, распределённой по равномерному закону. Ориентация преграды на поле выбирается также случайным образом согласно равномерному закону распределения. Вариантов ориентации всего два: горизонтальная или вертикальная.

В районе левой части поля случайным образом выбирается свободная клетка. Данную точку (клетку) обозначим как A. Её радиус-вектор \(\vec{r}_{\rm A}\). В правой части аналогичным образом определяется точка B с радиус-вектором \(\vec{r}_{\rm B}\).

  • Размеры левой области, где генерируется точка \(\vec{r}_{\rm A}\):

\[ x_{\rm min}^{\rm left} = 0, \quad x_{\rm max}^{\rm left} = \lfloor n/5 \rfloor, \quad y_{\rm min}^{\rm left} = 0, \quad y_{\rm max}^{\rm left} = m; \]

  • Размеры правой области, где генерируется точка \(\vec{r}_{\rm B}\):

\[ x_{\rm min}^{\rm right} = n - \lfloor n/5 \rfloor, \quad x_{\rm max}^{\rm right} = n, \quad y_{\rm min}^{\rm right} = 0, \quad y_{\rm max}^{\rm right} = m. \]

Из каждой клетки возможны четыре перемещения: вверх, вниз, вправо, влево. Или в географической формулировке: север (N), юг (S), восток (E), запад (W).

Задачи работы:

  1. Найти кратчайший путь из точки A в точку B, используя алгоритм эвристического поиска A*, и найти длину этого пути. При этом суммарное количество клеток поля (\(m \cdot n\)) не должно быть меньше 5000.

  2. Показать решение графически. Пример оформления графика показан на рисунке ниже.

Пример оформления графика

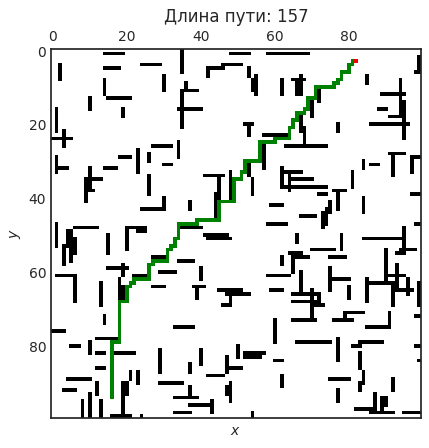
Требования к содержанию и оформлению отчёту всё те же.

Шаблон кода#

Подключение библиотек:

from numpy.random import Generator, PCG64
import matplotlib.pyplot as plt
import numpy as np
# Добавляйте др. необходимые вам пакеты
...

Для воспроизведения и сравнения результатов необходим генератор случайных чисел.

rs = Generator(PCG64(seed=1747))

Note

Если seed != None, а есть любое неотрицательное число, то при каждом запуске программы генератор будет выдавать одну и ту же последовательность чисел.

Функция создания карты (сетки)^

def create_empty_grid(size: tuple):
    """Создать пустую сетку размера size = (m, n)."""
    pass

Функция заполнения сетки препятствиями:

def fill_obstacles(grid, n, min_len, max_len):
    """Заполнить клеточное поле grid n препятствиями.
    
    Препятствие имеет случайную длину в диапазоне от min_len до max_len
    и единичную ширину.
    """
    pass

Функция генерации точки в свободной ячейке в заданной области:

def gen_point_in_area(grid, xlim, ylim, state):
    """Сгенерировать случайную точку в заданной области поля grid.

    Параметры xlim и ylim определяют размеры и положение области генерации точки.
    Параметр state определяет, является ли генерируемая точка исходной
    точкой A или целевой точкой B.
    """
    pass

Реализация алгоритма A*:

def calc_shortest_path(problem, w=1):
    """Поиск кратчайшего пути с помощью алгоритма A*.
    
    * problem - проблемное пространство (клеточное поле).
    * w - вес эвристики.
    """
    pass

Ниже приведены заделки функций, которые могут быть полезными в плане разбиения программы для улучшения читаемости:

def expand(problem, node, w):
    """Раскрыть узел node поля problem.
    
    w - весовой множитель эвристической функции.
    """
    pass

def calc_cost(s, d, c, w):
    """Рассчитать стоимость действия агента.
    
    * s - индекс (координата) (i, j) текущей ячейки.
    * d - индекс (i, j) целевой ячейки.
    * c - расстояние до текущей ячейки ("стоимость" текущей ячейки)
          от начальной.
    * w - весовой множитель эвристической функции.
    """
    pass

def heuristic(s, d):
    """Функция эвристики - расстояние до целевой ячейки d из текущей s."""
    pass

Пример исходных данных#

# Размеры (ширина и длина) поля
m, n = 100, 100
# Число препятствий
n_obs = 250
# min и max длины препятствий
obs_len = 3, 7
# Область пространства появления (точки A) и...
xlim0, ylim0 = [0, n // 5], [0, m]
# назначения объекта (точки B)
xlim1, ylim1 = [n - n // 5, n], [0, m]

Моделирование#

Функция запуска решателя задачи:

def simulate(*args):
    """Найти кратчайший путь из точки A в точку B."""
    pass

Вместо *args напишите свои аргументы.

Моделирование и получение результатов:

results = simulate(...)

Здесь вместо ... также ваши переменные и параметры.

Обработка результатов и визуализация#

Пример функции построения итогового графика:

def plot_grid(grid, ax=None, **kw):
    """Визуализировать клеточное поле grid`."""
    if ax is None:
        fig, ax = plt.subplots()
    ...
    return ax

Результат должен выглядеть примерно, как на рисунке ниже.

Пример графика

См. также#

В книге “Искусственный интеллект. Современный подход. Том 1” в главе 3 содержится подробная информация (описание и блок-схема) алгоритма А*. Эти знания могут сильно помочь вам в решении данной задачи.