Лабораторная работа №1. Клеточный автомат “Лесной пожар”#
Задача#
Эволюция лесного пожара описывается клеточным автоматом (КА).
Лес моделируется клеточным полем размером \(w \times h\). В \(n\) клетках поля изначально есть деревья: \(n = \eta \cdot w \cdot h\), в остальных клетках деревьев нет. Здесь \(\eta\) - заполненность поля деревьями: \(0 \le \eta \le 1\).
Цвета клеток поля КА должны соответствовать одному единственному состоянию. Например, цвет клетки с деревом зелёный, без дерева - чёрный, с горящим деревом - оранжевый.
Изначально имеется \(f\) горящих деревьев. Их координаты - ячейки - генерируются случайным образом.
Правила клеточного автомата:
Дерево, в окрестности которого есть хотя бы одно горящее дерево, загорается.
На месте сгоревшего дерева образуется пустая ячейка.
На месте пустой ячейки с вероятностью \(P_{\rm g}\) вырастает дерево, если в окрестности нет горящих деревьев.
Любое дерево может загореться с заданной вероятностью \(P_{\rm f}\).
Цель работы - закрепить знания и получить опыт создания и применения КА для моделирования различных процессов.
Задачи работы:
Запрограммировать КА, описывающий эволюцию горящего леса.
Исследовать процесс лесного пожара, накапливая статистику количества горящих \(a_{\rm f}\) и негорящих \(a_{\rm t}\) деревьев, пустых ячеек \(a_{\rm e}\) и др.
Исследовать влияние двух форм окрестности \(\Theta = \{\theta_+, \theta_\times\}\) (окрестность фон-Неймана и окрестность Мура соответственно) на процесс распространения пожара.
Обработав накопленную статистику, построить зависимость \(a_{\rm f}(t,\Theta,\ldots)\) распространения пожара в зависимости от времени \(t\), формы окресности \(\Theta\) и/или от других факторов.
Оценить производительность компьютерной модели.
Составить отчёт о лабораторной работе (ЛР). В отчёте ответьте на вопросы.
Варианты#
Группа делится на 4 варианта.
Общие исходные данные:
\(w = 200\);
\(h = 200\);
\(n = \eta \cdot w \cdot h\) при \(\eta = 0.8\);
\(f = 1\);
\(P_{\rm f} = 2 \cdot 10^{-5}\);
\(P_{\rm g} = 0.02\);
“затравка” (seed) генератора псевдослучайных чисел - \(1097\);
число итераций по времени - \(500\).
Изменения в исходных данных в зависимости от варианта:
вариант 1 - три различных значения вероятности воспламенения дерева: \(P_{\rm f} = \{2, 3, 4\} \cdot 10^{-5}\).
вариант 2 - варьируется вероятность вырастания нового дерева: \(P_{\rm g} = \{8, 16, 32\} \cdot 10^{-3}\).
вариант 3 - изменять начальную заполненность поля: \(\eta = \{\frac{1}{3}, \frac{2}{3}, 1\}\).
вариант 4 - рассмотреть различное число изначально горящих деревьев: \(f = \{1, 3, 9\}\).
Код#
Далее приведён шаблон кода, который может помочь в разработке КА.
Для начала импортируем библиотеки, которые точно понадобятся:
import matplotlib.pyplot as plt
import numpy as np
Также инициализируем наш глобальный генератор случайных чисел с заданной “затравкой” seed:
rs = np.random.RandomState(seed=1097)
Note
На практике полезно инициализировать генератор случайных чисел явно. Это позволяет воспроизводить результаты псевдослучайных процессов разными пользователями на различных устройствах, что важно, когда речь идёт о научном исследовании.
Возможные окрестности#
Окрестности КА можно описать с помощью класса перечисления Enum из стандартной библиотеки enum.
Для этого достаточно создать класс, унаследованный от Enum, и перечислить в нём состояния:
from enum import Enum
class NeighborhoodType(Enum):
CROSS = "+"
NEUMAN = "x"
Описание состояний клеток#
Поскольку число возможных состояний клеток конечно, описать эти состояния можно так же с помощью Enum:
class CellState(Enum):
EMPTY = 0
FIRING = 1
TREE = 2
Функция визуализации#
Опишем функцию визуализации КА.
Для начала создадим цветовую карту из трёх цветов: тёмно-серого (угольного), оранжевого и зелёного.
# Для создания цветовой карты из массива цветов
# нам понадобится конструктор ListedColormap
from matplotlib.colors import ListedColormap
# Массив из указанных трёх цветов...
colors = ["#49423D", "orange", "green"]
# и сама цветовая карта
cmap_forest = ListedColormap(colors)
Сопоставляем цвета с состояниями клетки: угольный - сгоревшее, оранжевый - горящее и зелёный - здоровое дерево.
class CellColor(Enum):
EMPTY = colors[0]
FIRING = colors[1]
TREE = colors[2]
Собственно, сама функция визуализации:
def plot_grid(ca, ax=None, **kw):
# ca - клеточный автомат (матрица)
if ax is None:
# Не был передан уже созданный график
fig, ax = plt.subplots()
# Визуализируем КА, используя нашу цветовую карту
ax.matshow(ca, cmap=cmap_forest)
# В ключевых аргументах kw можно передать заголовок графика,
# а можно не передавать. В последнем случае по умолчанию
# в title будет лежать пустая строка.
# В данной работе в title имеет смысл записать тип окрестности.
title = kw.get("title", "")
# Наводим красоту
ax.set(
xlabel="Length",
ylabel="Width",
title=title,
aspect="equal"
)
# Возвращаем построенный график
return fig, ax
График строится функцией matshow (matrix show).
В данном случае КА (ca) мы будем представлять в виде двухмерной матрицы.
В зависимости от числа в ячейке этой матрицы matshow назначит конкретный цвет из цветовой карты.
Например, при ca[3, 7] = 1 на графике в 4-й строке и 8-м столбце будет клетка с оранжевым цветом (FIRING).
На этом подготовительный этап заканчивается.
Создание и инициализация клеточного автомата#
Один из вариантов структуры данных для хранения КА - это матрица размера \(w \times h\). Для создания клеточного поля предлагается описать функцию:
def create_ca(w: int, h: int):
"""Создать однородную матрицу,
т.е. пустую матрицу или матрицу,
заполненную определённым значением.
* `w` и `h` - ширина и высота КА.
"""
pass
return ...
Attention
Здесь и далее вместо заглушки pass должна быть ваша реализация.
Вместо многоточих - имя вашей переменной (переменных).
Warning
Важно, чтобы итоговая матрица ca хранила числа типа int, а не float.
Иначе невозможно будет сравнивать значения на равенство ==.
Теперь необходимо задать начальное состояние КА ca - заполнить деревьями в количестве \(n = \eta \cdot w \cdot h\) и “поджечь” \(f\) случайных из них. Доступ к генераторам случайных чисел осуществляется через наш генератор rs, который может быть либо глобальным (как в данном случае), либо передаваться как аргумент функций (полезно и удобно в больших программах).
def init_state(ca: np.ndarray, eta: float, f: int):
"""Инициализировать начальное состояние КА,
т.е. в заданном количестве `eta*w*h` случайных
клеток разместить деревья и поджечь также случайным
образом `f` из деревьев.
* `ca` - клеточный автомат (матрица).
* `eta` - доля клеток с деревьями.
* `f` - число горящих деревьев.
"""
pass
Note
Функция init_state может изменять саму переданную матрицу ca, а может лишь использовать её для формирования новой матрицы, которую в таком случае функция должна вернуть.
Выбор вы делаете сами.
Главное, чтобы функция делала что-то одно.
Описание эволюции клеточного автомата#
# Для аннотации типов импортируем
# стандартные типы данных.
# Это упростит понимание того, аргументы
# какого типа должны принимать функции.
from typing import List, Tuple
def update(ca: np.ndarray, nt: NeighborhoodType):
"""Обновление всего КА.
* `ca` - матрица КА.
* `nt` - тип окрестности.
Возвращает новое состояние КА.
"""
pass
return ...
def update_cell(ca: np.ndarray,
new_ca: np.ndarray,
cell: Tuple[int, int],
neighbor_indexes: List[int]):
"""Обновление состояния заданной клетки `cell`
в соответствии с правилами эволюции КА.
Условия проверяются по матрице `ca`, т.е.
по КА в текущем состоянии.
Новое же состояние клетки записывается в
матрицу `new_ca`.
* `ca` - матрица КА.
* `new_ca` - матрица КА в новом состоянии.
* `cell` - кортеж, хранящий пару индексов `(i, j)`
текущей (рассматриваемой) ячейки КА.
* `neighbor_indexes` - список индексов
(кортежей пар индексов ячеек `(i, j)`) соседей
рассматриваемой ячейки `cell`.
"""
pass
def get_cross_neighborhood(cell: Tuple[int, int],
ca_shape: Tuple[int, int]):
"""Вернуть индексы окрестных ячеек клетки `cell = (i, j)`
для случая "+"-окрестности.
Размеры КА `ca_shape = (h, w)` используются для определения
индексов, вышедших за границы КА (массива `ca`).."""
pass
# Вернуть индексы окрестных ячеек
return ...
def get_neuman_neighborhood(cell: Tuple[int, int],
ca_shape: Tuple[int, int]):
"""Вернуть индексы окрестных ячеек клетки `cell = (i, j)`
для случая окрестности фон-Неймана.
Размеры КА `ca_shape = (h, w)` используются для определения
индексов, вышедших за границы КА (массива `ca`).
"""
pass
return ...
В процессе моделирования необходимо сохранять данные для формирования статистики. Для упрощения этой задачи можно завести отдельный класс с функциональностью добавления, хранения и визуализации статистики:
class Statistics:
def __init__(self):
# Массив шагов по времени
self.t = []
# Количество горящих деревьев на временных шагах
self.a_f = []
# Количество здоровых деревьев на временных шагах
self.a_t = []
# Количество пустых клеток на временных шагах
self.a_e = []
def append(self, t: int, ca: np.ndarray):
"""Добавить состояние КА `ca` в момент времени `t`."""
pass
def plot_firing_time(self, ax=None, **kw):
"""График числа горящих деревьев от времени."""
if ax is None:
_, ax = plt.subplots()
pass
return ax
def plot_trees_time(self, ax=None, **kw):
"""График числа здоровых деревьев от времени."""
if ax is None:
_, ax = plt.subplots()
pass
return ax
def plot_empty_time(self, ax=None, **kw):
"""График числа пустых клеток от времени."""
if ax is None:
_, ax = plt.subplots()
pass
return ax
Запуск моделирования#
Для запуска моделирования предлагается описать отдельную функцию, принимающую на вход КА ca и тип окрестности neighborhood_type и возвращающую накопленную статистику:
def simulate(ca: np.ndarray,
nt: NeighborhoodType,
time: int):
"""Смоделировать процесс лесного пожара.
* `ca` - матрица начального состояния КА.
* `nt` - тип окрестности.
* `time` - число шагов моделирования по времени
(время моделирования).
"""
st = Statistics()
# В цикле по времени от 0 до time
# вызываем функцию обновления КА
# и добавляем результат в статистику stats.
pass
return st
Последовательность моделирования проста:
Инициализируем исходные данные:
# "Затравка" для генератора псевдослучайных чисел
seed = 1097
# Размеры клеточного поля
w, h = 200, 200
# Доля клеток с деревьями
eta = 0.8
# Число изначально горящих деревьев
f = 1
# Вероятность вырастания нового дерева
p_g = 0.02
# Вероятность случайного воспламенения дерева
p_f = 2e-5
# Модельное время (число обновлений автомата)
sim_time = 500
Создаём КА и запускаем симуляцию:
# Создаём "пустой" КА
ca = create_ca(w, h)
# Задаём начальное состояние КА
init_state(ca, eta, f)
# Также стоит запомнить исходное состояние
initial_ca = np.copy(ca)
# Симулируем.
# В данном случае рассматриваем "+"-окрестность
st = simulate(ca, NeighborhoodType.CROSS, time=500)
# Обрабатываем результаты, строим графики и пр.
pass
Ожидаемый результат работы#
Ожидаемый результат моделирования представлен на картинках ниже.
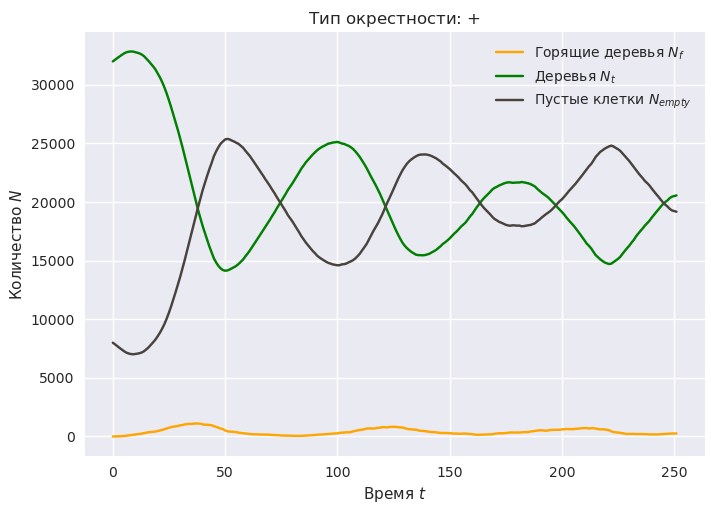
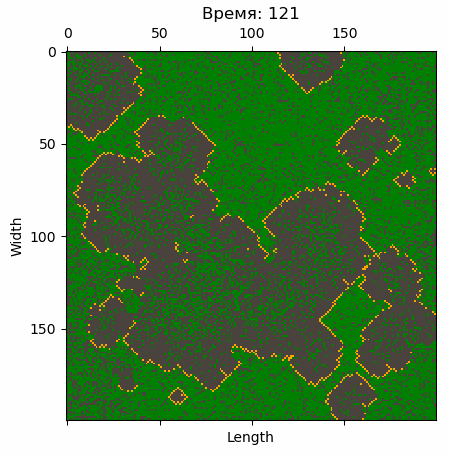
С помощью Python несложно сделать анимацию эволюции КА.
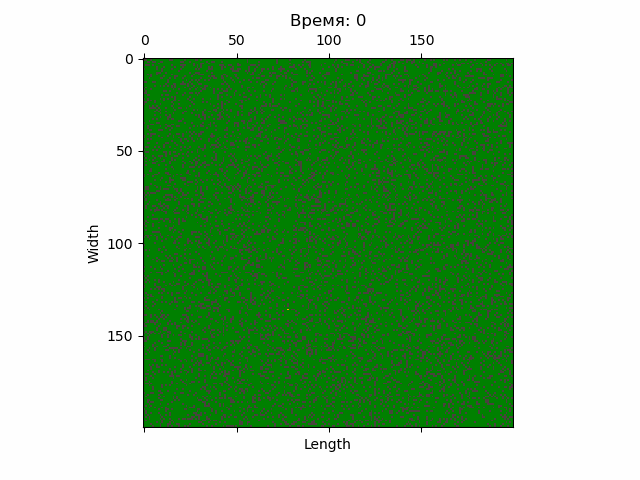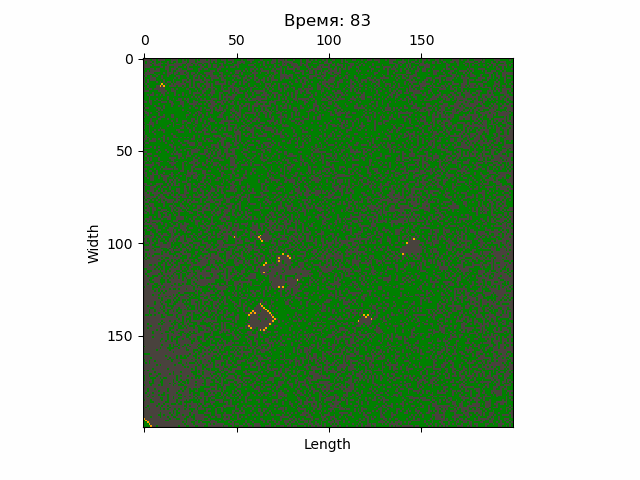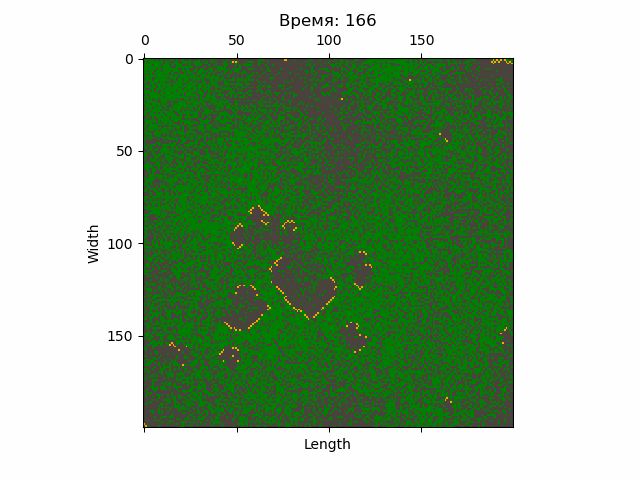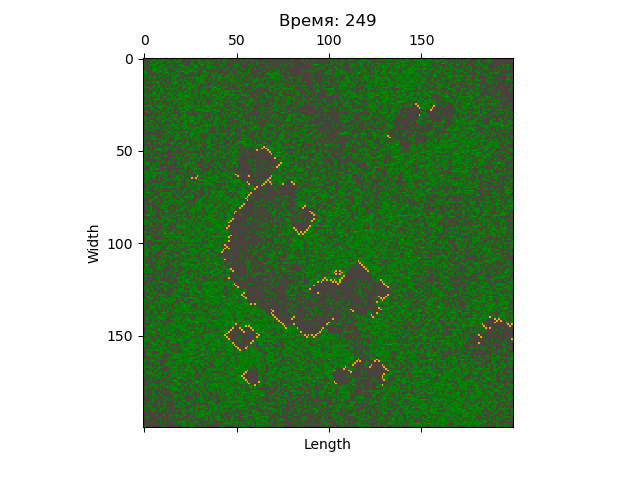
Также стоит обработать статистику, получив конкретные числа, например, среднее количество горящих деревьев, среднее квадратическое отклонение этого количества и т.п. Полезные инструмент для этого содержатся в модуле stats пакета SciPy.
Вопросы#
По вашему мнению, достаточно ли реалистична разработанная модель лесного пожара?
Можно ли её усовершенствовать, сделав более реалистичной?
Достаточна ли вычислительная производительность программы на ваш взгляд? Можно ли её улучшить? Как?
См. также#
Построение графиков matplotlib подробнее описано в справочнике кафедры СМ6.
Для обработки статистики крайне полезным инструментом является модуль
statsиз пакета SciPy.
