Лабораторная работа №2. Дискретно-событийное моделирование на примере задачи вулканической баллистики

Лабораторная работа №2. Дискретно-событийное моделирование на примере задачи вулканической баллистики#

Цель работы - закрепить знания и получить опыт решения физической задачи путём компьютерного моделирования с применением дискретно-событийного подхода.

Основы использования библиотеки дискретно-событийного моделирования SimPy см. в справочнике.

Описание задачи#

Смоделировать процесс разлёта камней из кратера вулкана при его извержении, получив в результате координаты точек падения камней на горизонтальную плоскость \(z=0\). Пространство трёхмерно, оси \(Ox\) и \(Oy\) лежат в горизонтальной плоскости, ось \(Oz\) направлена вертикально вверх.

Процесс извержения характеризуется следующими параметрами:

\(H > 0\) - высота вулкана;
\(D_{\rm c}\) - глубина кратера относительно вершины вулкана;
\(R_{\rm c}\) - радиус кратера;
\(\mu_v\) и \(\sigma_v\) - параметры нормального распределения величины скорости камней: \(v = \|\vec v\| \sim \mathcal{N}(\mu_v, \sigma_v)\), где \(\vec v\) - вектор скорости камня;
\(\varphi \in [0, 2\pi]\) - диапазон разлёта бомб по углу азимута;
\(\mu_\theta\) и \(\sigma_\theta\) - параметры нормального распределения угла возвышения (наклона к горизонту) вектора скорости камней: \(\theta \sim \mathcal{N}(\mu_\theta, \sigma_\theta)\);
\(R_{\rm min}\) и \(R_{\rm max}\) - минимальный и максимальный радиусы бомб. Распределение величины радиуса камня - равномерное;
\(\rho\) - плотность материала камней;
\(\beta_{\rm erup}\) - среднее время между выбросами камней при извержении. Случайная величина временного промежутка между выбросами \(\Delta t_{\rm erup}\) распределена по экспоненциальному закону с параметром \(\beta_{\rm erup}\).

Задачи работы:

Создать компьютерную модель процесса извержения вулкана. Реализовать возможность моделирования с учётом и без учёта столкновения между камнями.
Составить отчёт по лабораторной работе (ЛР). Требования к отчёту см. во введении. Привести значения параметров (исходных данных и пр.) модели, полученные результаты в виде графика аналогичного графику, показанному на лекциях, а также проанализировать полученные результаты.

Important

Используйте дискретно-событийный подход к моделированию извержения. В этом может помочь библиотека SimPy.

Методические указания#

Предполагается, что все камни (бомбы) имееют форму шара. Радиусы \(R\) камней случайны и подчиняются равномерному закону распределения: \(R \in [R_{\rm min}; R_{\rm max}]\). Масса камня \(m = \rho V = \rho \cdot \frac{4}{3} \pi R^3\). Его траектория описывается радиус-вектором \(\mathbf{r} = (\ \begin{matrix} x & y & z \end{matrix} )\) и вектором скорости \(\mathbf{v} = \mathrm{d} \mathbf{r} / \mathrm{d} t = ( \begin{matrix} v_x & v_y & v_z \end{matrix} )\).

Начальные положение и скорость камня#

Исходя из условия задачи, необходимо сгенерировать случайные радиус-вектор (координаты) \(\mathbf{r}_0\) и вектор начальной скорости камня \(\mathbf{v}_0\).

Начальный радиус-вектор камня: \(\mathbf{r}_0 = (\begin{matrix}x_0 & y_0 & z_0 \end{matrix})\). Для его получения можно сгенерировать случайную (с равномерным законом) величину расстояния \(d\) камня от оси кратера в пределах от \(0\) до \(R_{\rm c}\). Затем сгенерировать случайный угол азимута \(\alpha\), распределённый равномерно от \(0\) до \(2 \pi\). Данный угол отсчитывается от положительного направления оси \(Ox\). Глубина (координата \(z_0\)) камня - случайная величина с равномерным распределением от \(H - D_{\rm c}\) до \(H\). По полученным значениям формируем начальный радиус-вектор камня:

\[ \mathbf{r}_0 = ( \begin{matrix} d \cos{\alpha} & d \sin{\alpha} & z_0 \end{matrix} ). \]

Далее, формируем случайный вектор начальной скорости. Величина (длина) этого вектора \(v_0\) - случайная величина, распределённая по нормальному закону (см. условие задачи). Также, согласно условию задачи, генерируются случайные величины углов \(\varphi\) и \(\theta\). Угол азимута \(\varphi\) отсчитывается от положительного направления оси \(Ox\), угол места \(\theta\) - от горизонтальной плоскости в положительном направлении оси \(Oz\). Вектор скорости тогда:

\[ \mathbf{v}_0 = ( \begin{matrix} v_0 \cos{\theta} \cos{\varphi} & v_0 \cos{\theta} \sin{\varphi} & v_0 \sin{\theta} \end{matrix} ). \]

Тем самым мы однозначно определили траекторию движения камня.

Свободный полёт камня#

Сопротивление воздуха не учитывается. Следовательно, все камни летят по параболам как тела, брошенные под углом к горизонту. Зная начальное положение каждого камня \(\mathbf{r}_0\) и вектор его начальной скорости \(\mathbf{v}_0\), мы знаем всю траекторию движения камня:

(1)#\[ \mathbf{r}(\tau) = \mathbf{r}_0 + \mathbf{v}_0 \tau + \cfrac{\mathbf{g} \tau^2}{2}, \]

\[ \mathbf{v}(\tau) = \cfrac{\mathrm{d} \mathbf{r}}{\mathrm{d} \tau} = \mathbf{v}_0 + \mathbf{g} \tau, \]

где \(\mathbf{r}\) - радиус-вектор (координата) камня: \(\mathbf{r} = ( \begin{matrix} x & y & z \end{matrix} )\); \(\mathbf{g}\) - вектор ускорения свободного падения: \(\mathbf{g} = ( \begin{matrix} 0 & 0 & -9.81 \end{matrix} )\) м/с\(^2\); \(\tau\) - относительное время полёта камня: \(\tau = t - t_0\); \(t\) - глобальное время - обновляется обработчиком событий; \(t_0\) - глобальное время вылета камня из кратера.

Время вылета камня \(t_0\) - это время соответствующего выброса \(t_{\rm erup}\), которое, согласно условию задачи, является случайной величиной с экспоненциальным законом распределения. Условимся, что первый выброс происходит в самом начале, т.е. при \(t = 0\). Следующий выброс случится через случайный промежуток времени \(\Delta t_{\rm erup}\), причём функция плотности вероятности величины этого промежутка имеет вид:

\[ \rho_{\rm erup}(\Delta t_{\rm erup}) = \cfrac{1}{\beta_{\rm erup}} \exp{\left( -\cfrac{\Delta t_{\rm erup}}{\beta_{\rm erup}} \right)}. \]

Аналогично получается случайный промежуток времени между вторым и третьим выбросом, третьим и четвёртым и т.д. Другими словами, время выброса камней в некотором \(n\)-м выбросе, \(n > 0\), есть:

\[ t_{0 n} = \sum\limits_{i=0}^{n-1}{\Delta t_{{\rm erup} \, i}}, \]

причём \(\Delta t_{{\rm erup} \, 0} = 0\). Относительное время при этом: \(\tau_n = t - t_{0 n}\).

Зная траекторию, мы можем вычислить время, через которое камень упадёт на землю (когда \(z=0\)). Для этого нужно решить квадратное уравнение (1) относительно \(\tau\) и выбрать корень \(\Delta \tau_{\rm g}\), имеющий физический смысл, т.е. \(\Delta \tau_{\rm g} > 0\). Учтя, что камни вылетают из кратера в направлении “вверх” (\(v_{0z} > 0\)) и проекция \(g_z\) всегда отрицательна, получим:

\[ \Delta \tau_{\rm g} = \cfrac{-v_{0z} - \sqrt{v_{0z}^2 - 2 g_z z}}{g_z}, \]

где нижними индексами \(z\) обозначены проекции векторов на вертикальную ось \(Oz\). Рассчитываемая таким образом задержка вдальнейшем используется для создания события приземления камня.

Далее необходимо научиться учитывать столкновения камней. Для этого сначала сформируем метод расчёта времени столкновения, а затем построим модель столкновения на основе закона сохранения импульса.

Расчёт времени столкновения камней#

Рассмотрим два камня 1 и 2. Условием столкновения камней является сближение их центров на расстояние, равное сумме их радиусов, т.е.:

\[ \| \mathbf{r}_2(t_{\rm col}) - \mathbf{r}_1(t_{\rm col}) \| = R_1 + R_2 \]

или, возведя обе части в квадрат,

(2)#\[ \| \mathbf{r}_2(t_{\rm col}) - \mathbf{r}_1(t_{\rm col}) \|^2 - (R_1 + R_2)^2 = 0, \]

где \(t_{\rm col}\) - момент (глобального) времени столкновения камней. Уравнение (1) для условия (2) не подходит, т.к. сталкиваться могут любые летящие камни, в том числе и вылетевшие в разных выбросах. Следовательно, относительное время камней может быть различным: \(\tau_1 \ne \tau_2\). Поэтому уравнение движения (1) нужно записать в глобальном времени:

(3)#\[ \mathbf{r}(t) = \mathbf{r}_0 + \mathbf{v}_0 (t - t_0) + \cfrac{\mathbf{g} (t - t_0)^2}{2}. \]

Important

Важно помнить, что камни разичных выбросов имеют собственное значение времени выброса \(t_0\).

Таким образом, подставляя уравнение движения (3) в условие столкновения двух камней (2), получаем уравнение, из которого можем получить время столкновения \(t_{\rm col}\). Расписав это векторное уравнение по координатам, получим:

(4)#\[\begin{split} \begin{split} & [x_{2 \, 0} + v_{2x \, 0} (t_{\rm col} - t_{2 \, 0}) - x_{1 \, 0} - v_{1x \, 0} (t_{\rm col} - t_{1 \, 0})]^2 \\ & + [y_{2 \, 0} + v_{2y \, 0} (t_{\rm col} - t_{2 \, 0}) - y_{1 \, 0} - v_{1y \, 0} (t_{\rm col} - t_{1 \, 0})]^2 \\ & + \left[ z_{2 \, 0} + v_{2z \, 0} (t_{\rm col} - t_{2 \, 0}) + \cfrac{g_z (t_{\rm col} - t_{2 \, 0})^2}{2} - z_{1 \, 0} - v_{1z \, 0} (t_{\rm col} - t_{1 \, 0}) - \cfrac{g_z (t_{\rm col} - t_{1 \, 0})^2}{2} \right]^2 \\ & - (R_1 + R_2)^2 = 0. \end{split} \end{split}\]

Это квадратное уравнение относительно времени \(t_{\rm col}\). Отыскание корня в этом случае - задача несложная, требующая только внимательности и аккуратности.

Note

Решить уравнение (4) можно и численно, однако в реальных задачах это является дополнительной вычислительной нагрузкой. Если можно сформулировать точное решение, то лучше дать вычислителю готовую формулу, чем заставлять его итеративно искать приближённое решение. В данном случае уравнение простое, и численное решение может быть таким же быстрым, как и аналитическое, которое в данном случае имеет довольно громоздкий вид.

Note

Способы численного решения уравнений в Python можно найти в справочнике.

При расчёте времени столкновения возможны следующие случаи:

Вещественного корня нет - траектории камней не пересекаются.
Время столкновения больше времени полёта одного из камней - один из камней упадёт раньше, чем столкнётся.
Время столкновения меньше, чем время начала полёта одного из камней - один из камней в рассчитанный момент времени ещё лежал в кратере.
В рассчитанный момент времени оба камня находятся в полёте.

Из всех перечисленных случаев интерес представляет только последний. Рассчитав время столкновения для всех пар летящих камней, мы выбираем ближайший момент времени - это и будет ближайшим событием типа “столкновение”.

Получив таким образом время \(t_{\rm col}\), мы можем рассчитать координаты \(\mathbf{r}_{\rm col}\) и скорости \(\mathbf{v}_{\rm col}\) сталкивающихся камней непосредственно перед столкновением.

Модель столкновения камней#

Модель столкновения двух камней основана на законе сохранения импульса.

Величина скорости сближения (closing) тел в момент удара

\[ v_{\rm c} = \left( \mathbf{v}_{{\rm col} 2} - \mathbf{v}_{{\rm col} 1} \right) \cdot \mathbf{n}, \]

где \(\mathbf{n}\) - вектор единичной нормали при столкновении:

\[ \mathbf{n} = \cfrac {\mathbf{r}_{{\rm col} 1} - \mathbf{r}_{{\rm col} 2}} {\| \mathbf{r}_{{\rm col} 1} - \mathbf{r}_{{\rm col} 2} \|} = \cfrac {\mathbf{r}_{{\rm col} 1} - \mathbf{r}_{{\rm col} 2}} {R_1 + R_2}. \]

Note

Как известно, скалярное произведение двух векторов - это проекция длины одного вектора на направление другого. В данном случае речь идёт о проекции разности скоростей камней на направление (единичный вектор) общей нормали.

Скорость разлёта (separating) тел до и после столкновения соответственно:

\[ v_{\mathrm{s} 0} = -v_{\rm c} \]

\[ v_{\rm s} = k_p v_{\rm c}, \]

где \(k_p\) - коэффициент восстановления: \(k_p \in [0; 1]\).

Изменение скорости при ударе:

\[ \Delta v_{\rm s} = v_{\rm s} - v_{\mathrm{s} 0}. \]

Вектор полного импульса:

\[ \mathbf{p} = \cfrac{m_1 m_2}{m_1 + m_2} \Delta v_{\rm s} \mathbf{n}. \]

Следовательно, исходя из закона сохранения импульса, возможно рассчитать скорость каждого тела после столкновения:

\[ \mathbf{v}_1' = \mathbf{v}_1 + \cfrac{\mathbf{p}}{m_1}, \]

\[ \mathbf{v}_2' = \mathbf{v}_2 - \cfrac{\mathbf{p}}{m_2}. \]

Note

Знаки в представленных расчётных формулах необходимо строго соблюдать. Знаки проекций векторных величин нас не интересуют - они могут быть любыми. Обычная векторная алгебра.

Обновление траекторий столкнувшихся камней#

При наступлении события “столкновение” важно сделать следующее:

Заменить начальный радиус-вектор \(\mathbf{r}_0\) и вектор начальной скорости \(\mathbf{v}_0\) двух камней на \(\mathbf{r}(t_{\rm col})\) (согласно (3)) и \(\mathbf{v}'\) соответственно. Также необходимо заменить время \(t_0\) каждого камня на время столкновения \(t_{\rm col}\). Тем самым мы сможем строить траектории камней после их столкновения.
Для столкнувшихся камней пересчитать моменты времени их падения на землю и создать соответствующие события типа “приземление”. При этом все предыдущие события и процессы для этих камней необходимо удалить из очереди событий. Делается это с помощью метода interrupt объекта события (класса simpy.Event). Для упрощения задачи рекомендуется все события и процессы ассоциировать с конкретным камнем, например, с помощью словаря (см. словарь processes в разделе Шаблон кода).
Для всех пар летящих камней пересчитать время ближайшего столкновения. Уже столкнувшиеся камни ничем принципиально не отличаются от всех остальных - они вновь могут столкнуться с любыми другими летящими камнями.

Указания к реализации дискретно-событийной модели#

Предлагается создать программу моделирования на основе библиотеки для дискретно-событийного моделирования SimPy. Основы написания программ с её использованием вы найдёте в справочнике.

В сформированной модели определены три типа событий:

выброс - ERUPTION;
приземление камня - GROUND;
столкновение двух камней - COLLISION.

Какие действия каким событиям соответствуют:

при каждом выбросе - событии ERUPTION - генерируется определённое число камней, который сразу же добавляются в список летящих бомб flyings. “Генерация” камней означает их инициализацию (см. конструктор класса Bomb в разделе Шаблон кода);
при приземлении - событии GROUND - упавший камень удаляется из списка flyings и добавляется в список упавших fallens;
при столкновении - событии COLLISION - необходимо рассчитать новые траектории столкнувшихся камней согласно методике, описанной в подразделах Расчёт времени столкновения камней и Модель столкновения камней. Затем произвести действия, описанные в подразделе Обновление траекторий столкнувшихся камней. За очистку событий и процессов, связанных с тем или иным камнем, отвечает функция clear_queue (см. раздел Шаблон кода). Для того, чтобы можно было прерывать собственные, т.е. написанные вами, процессы, в их генераторных функциях должен быть прописан блок try-except, обрабатывающий исключение типа simpy.Interrupt. Это исключении инициируется при вызове метода interrupt у объекта класса simpy.Event или simpy.Process.

В классе камня Bomb можно предусмотреть флаг is_collided, который бы говорил о том, сталкивался ли камень (True) или нет (False). Это поможет в задаче визуализации результатов (см. Визуализация).

В модели необходимы следующие процессы (в терминах SimPy):

eruption - порождает новые камни по истечении времени \(\Delta t_{\rm erup}\). Первый выброс происходит в начальный момент времени \(t = 0\).
collision - процесс, ожидающий момента столкновения камня с другим, т.е. наступления события COLLISION. В ответ на это событие инициирует действия: обновление траекторий, пересчёт моментов времени падения и столкновений и т.д.
ground - процесс, ожидающий падения камня - наступления события GROUND. В ответ на это событие перемещает упавший камень из списка fluings в список fallens.

Шаблон кода#

Подключим необходимые и/или полезные библиотеки:

from numpy.random import Generator, default_rng
from scipy.optimize import root_scalar
from typing import Dict, List
import matplotlib.pyplot as plt
import numpy as np
import simpy as sim

Класс бомбы:

class Bomb:
    def __init__(self,
                 t_erup: float,
                 r0: np.ndarray,
                 v0: np.ndarray,
                 mass: float,
                 radius: float):
        self.t_erup = t_erup
        self.r = r0
        self.v = v0
        self.m = mass
        self.R = radius
        # TODO: + ваши поля, которые посчитаете нужным использовать
        ...
    
    def calc_r(self, t: float):
        """Рассчитать радиус-вектор в момент времени `t`."""
        pass
    
    def calc_v(self, t: float):
        """Рассчитать вектор скорости в момент времени `t`."""
        pass
    
    def is_collided(self):
        """Столкивался ли камень."""
        pass
    
    def xy_fall(self):
        """Координаты точки падения."""
        pass

Глобальные списки летящих камней и камней на земле, а также словарь (хэш-таблица) процессов каждого экземпляра бомбы:

flyings, fallens = [], []
processes: Dict[Bomb, List[sim.Process]] = {}

Note

Запись processes: Dict[Bomb, List[sim.Process]] означает, что мы объявляем словарь, ключи которого имеют тип Bomb, а значения - тип sim.Process (процесс в SimPy).

Important

Ключи для словарей должны быть хешируемыми, т.е. уникальными. В классе Bomb нет реализации функции __hash__, но она и не нужна. За уникальность экземпляров Bomb отвечает адрес памяти, в которой каждый конкретный экземпляр хранится.

Генератор псевдослучайных чисел инициализируется, например, так:

rs = default_rng()

Note

Подробнее о генераторах псевдослучайных чисел можно почитать в справочнике.

Генераторная функция (функция-процесс) выброса камней при извержении:

def eruption(env: sim.Environment,
             dt: float,
             n: int,
             rs: Generator):
    """Процесс (в терминах SimPy) выброса камней.
    
    env :
        Объект среды SimPy,
        отвечающий за управление и обработку событий.
    dt :
        Время между выбросами.
    n :
        Число выбрасываемых камней.
    rs :
        Генератор чисел.
    """
    # Ожидание события ERUPTION...
    yield env.timeout(dt)
    # и вот оно наступило.
    # TODO: действия при наступлении события ERUPTION
    ...

Всего таких процессов при моделировании \(N_{\rm erups}\).

Функция генерации камней:

def gen_bombs(env: sim.Environment,
              n: int,
              rs: Generator):
    """Сгенерировать `n` бомб (камней).

    env :
        Объект среды SimPy,
        отвечающий за управление и обработку событий.
    n :
        Число выбрасываемых камней.
    rs :
        Генератор чисел.
    """
    pass

Функция-процесс, описывающая действие при наступлении события COLLISION:

def collision(env: sim.Environment, dt: float, b1: Bomb, b2: Bomb):
    """Процесс (в терминах SimPy),
    происходящий при наступлении события COLLISION.
    
    env :
        Объект среды SimPy,
        отвечающий за управление и обработку событий.
    dt :
        Задержка начала процесса.
    b1 и b2 :
        Бомбы.
    """
    try:
        yield env.timeout(dt)
        # TODO: действия при наступлении события столкновения
        ...
    except sim.Interrupt:
        return

Функция очистки очереди событий, связанных с бомбой b:

def clear_queue(b: Bomb):
    for proc in processes[b]:
        try:
            proc.interrupt()
        except RuntimeError:
            continue

Функция расчёта времени падения камня на землю (\(z=0\)):

def when_ground(b: Bomb):
    pass

Функция расчёта скоростей бомб b1 и b2 после их столкновения в момент времени t:

def calc_collision(t: float, b1: Bomb, b2: Bomb):
    pass

Функция расчёта момента времени столкновения \(t_{\rm col}\) камня b1 с камнем b2:

def when_collision(b1: Bomb, b2: Bomb):
    pass

Функция-процесс моделирования извержения:

def simulate(env: sim.Environment,
             n_erups: int,
             allowed_collisions: bool):
    """Процесс моделирования.
    
    env :
        Объект среды SimPy,
        отвечающий за управление и обработку событий.
    n_erups :
        Число выбросов.
    allowed_collisions :
        Столкновения учитываются (True) или нет (False).
    """
    pass

Экземпляр среды SimPy должен создаваться единожды и передаваться во все функции, в которых он требуется. Инициализация среды происходит просто:

env = sim.Environment()

Таким образом, создав экземпляр sim.Environment, вы вызываете функцию simulate(...) с заданными вами параметрами. Она в свою очередь инициализирует все необходимые процессы и запускает симуляцию внутри SimPy путём вызова env.run().

Визуализация#

Универсальная функция визуализации точек падения камней:

def top_view(xy: np.ndarray, ax=None, **kw):
    if ax is None:
        _, ax = plt.subplots()
    marker = kw.get("marker", ".")
    color = kw.get("color", "k")
    label = kw.get("label", "")
    alpha = kw.get("alpha", 1.)
    ax.plot(xy[:, 0], xy[:, 1],
            ls="", marker=marker, c=color, alpha=alpha, label=label)
    return ax

Пример итогового графика показан на рисунке ниже:

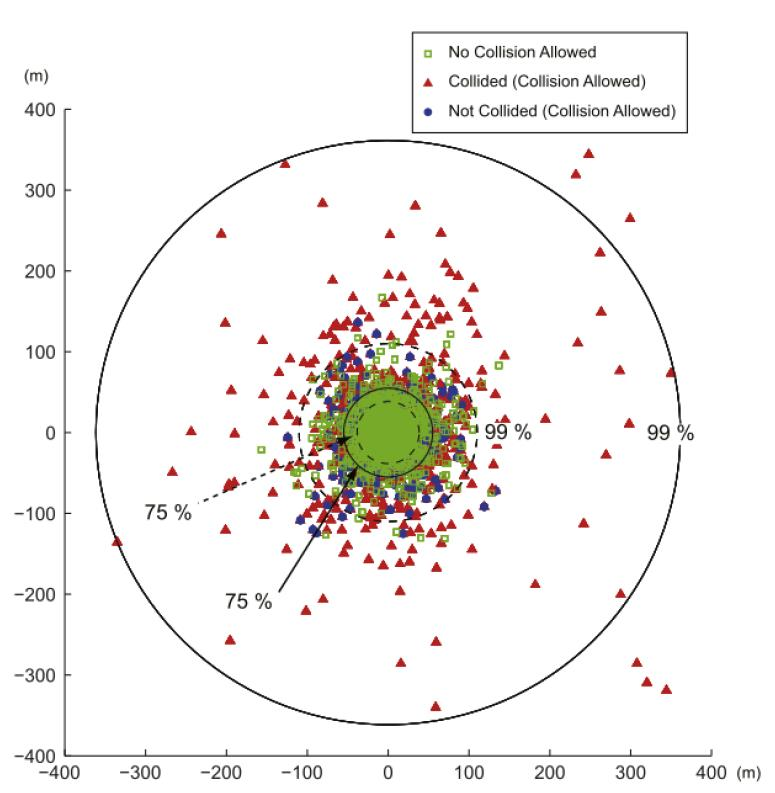
Пример результата

См. также#

Основы генераторов и итераторов приведены в справочнике. Там же описаны основы использования библиотеки SimPy.
Библиотека фреймворка дискретно-событийного моделирования SimPy.
Численное решение уравнений можно найти в справочнике. Там же содержатся основы построения графиков.
Требования к отчёту см. в разделе “Актуальная информация” в группе кафедры и во введении.

Лабораторная работа №2. Дискретно-событийное моделирование на примере задачи вулканической баллистики

Contents

Лабораторная работа №2. Дискретно-событийное моделирование на примере задачи вулканической баллистики#

Описание задачи#

Методические указания#

Начальные положение и скорость камня#

Свободный полёт камня#

Расчёт времени столкновения камней#

Модель столкновения камней#

Обновление траекторий столкнувшихся камней#

Указания к реализации дискретно-событийной модели#

Шаблон кода#

Визуализация#

Рекомендации#

См. также#