Лабораторная работа №3. Задачи дискретной и непрерывной оптимизации

Лабораторная работа №3. Задачи дискретной и непрерывной оптимизации#

Для решения задач необходимо работать с документацией применяемых библиотек и их функций.

Ниже приведены варианты заданий для подгрупп. Каждая подгруппа выбирает конкретный вариант и договаривается с другими подгруппами, чтобы не было пересечений между подгруппами.

Вариант 1 - Задача о рюкзаке#

Цель - закрепить знания, полученные на лекции по задачам дискретной оптимизации.

Задача - рассмотреть и проанализировать различные подходы к решению задачи о рюкзаке, являющейся задачей дискретной оптимизации.

Решить задачу о рюкзаке методами полного перебора, динамического программирования, жадным алгоритмом и случайным выбором.

В отчёте также отразить особенности, достоинства и недостатки каждого из указанных подходов к решению задачи и сравнить их вычислительную эффективность.

Вариант 2 - Оптимизация трёхступенчатого клина#

Цель - закрепить знания, полученные на лекции по задачам непрерывной оптимизации.

Задача - решить задачу непрерывной оптимизации с ограничениями.

Трёхступенчатый клин обтекается сверхзвуковым потоком воздуха.

Графически построить зависимость коэффициента восстановления полного давления $σ_{Σ}$ от углов ступеней клина $β_{1}$ и $β_{2}$ , построить её графически. Угол $β_{3}$ фиксирован. В каждой точке зависимости система скачков должна существовать (не должно быть отошедших скачков).
Определить углы $β_{1}^{*}$ и $β_{2}^{*}$ , соответствующие максимальному значению коэффициента восстановления полного давления, то есть

(5)#

{β_{1}^{*}, β_{2}^{*}} = \underset{0 < β_{1}, β_{2} < 2 π}{\arg \max} σ_{Σ} (β_{1}, β_{2})

Исходные данные: известна скорость набегающего потока $M_{1} = 3$ и угол 3-й ступени клина $β_{3} = 33^{\circ}$ . Показатель адиабаты воздуха $k = 1.4$ .

Ниже приведены расчётные формулы.

(6)#

\tan Δ β_{i} = \frac{\sin^{2} ν_{i} - \frac{1}{M_{i}^{2}}}{\frac{k + 1}{2} - (\sin^{2} ν_{i} - \frac{1}{M_{i}^{2}})} \cot ν_{i};

(7)#

Δ β_{i} = β_{i} - β_{i - 1};

(8)#

λ_{i + 1} = λ_{i} \cdot \frac{\cos ν_{i}}{\cos (ν_{i} - Δ β_{i})};

(9)#

\begin{array}{r} \begin{aligned} σ_{i} & = \frac{p_{0, i + 1}}{p_{0, i}} = \\ = \frac{{(\frac{k + 1}{2})}^{\frac{k + 1}{k - 1}}}{{(\frac{1}{M_{i}^{2} \sin^{2} ν_{i}} + \frac{k - 1}{2})}^{\frac{k}{k - 1}} {(k M_{i}^{2} \sin^{2} ν_{i} - \frac{k - 1}{2})}^{\frac{1}{k - 1}}}; \end{aligned} \end{array}

(10)#

σ_{Σ} = \prod_{i = 1}^{3} σ_{i} .

Вспомогательные формулы:

(11)#

M (λ) = λ \cdot \sqrt{\frac{\frac{2}{k + 1}}{1 - \frac{k - 1}{k + 1} λ^{2}}};

λ (M) = M \cdot \sqrt{\frac{\frac{k + 1}{2}}{1 + \frac{k - 1}{2} M^{2}}};

На рисунках ниже представлены расчётная схема и условие отрыва скачка уплотнения (СУ) от обтекаемого тела (зависимость угла СУ от угла поворота потока).

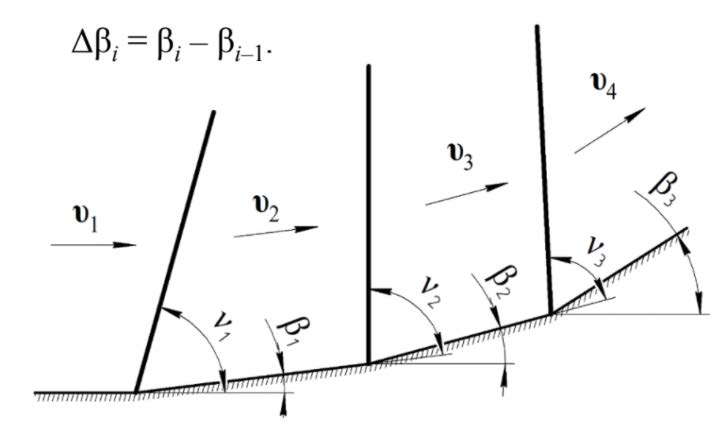
_images/clin-scheme.png — Fig. 1 Расчётная схема#

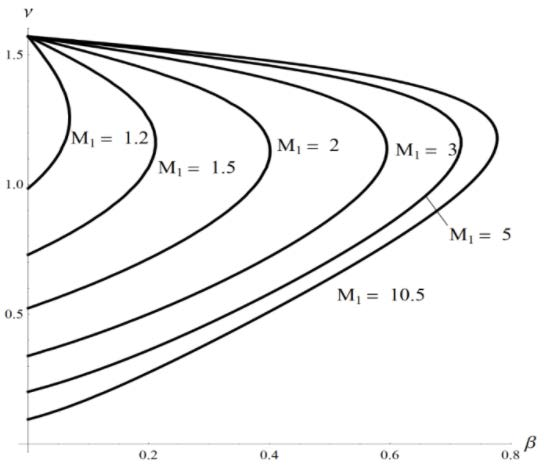
_images/avulsion.png — Fig. 2 Условие отрыва скачка уплотнения#

Important

На Условие отрыва скачка уплотнения $β_{i} \equiv Δ β_{i}$ и $ν_{i}$ - угол СУ.

Алгоритм расчёта следующий:

Из уравнения (6) при известном согласно (7) угле $Δ β_{1}$ и по исходному $M_{1}$ численно ищется значение угла СУ $ν_{1}$ на первой ступени клина.
По формуле (9) рассчитывается $σ_{1}$ для первого СУ.
Скорость потока за текущим СУ рассчитывается по формулам (8) и (11).
Алгоритм начинается заново для следующей ступени с учётом (7).

В итоге по формуле (10) рассчитывается коэффициент восстановления полного давления $σ_{Σ}$ .

Для решения задачи оптимизации (5) необходимо выбрать метод, например, из модуля optimize библиотеки научных расчётов SciPy.

Вариант 3 - Безопасное размещение склада боеприпасов#

Цель - рассмотреть возможные подходы к решению поставленной задачи поисковой непрерывной оптимизации.

Задача - решить задачу непрерывной поисковой оптимизации, используя как можно более эффективный алгоритм.

Имеется $n$ городов, заданных координатами на плоскости. Военным необходимо разместить большой (а потому опасный) склад боеприпасов в районе этих городов для надёжной защиты государства.

Требуется:

Сформулировать понятие “место безопасного размещения” склада боеприпасов.
Придумать или выбрать алгоритмом решения задачи.
Определить координаты места безопасного размещения склада боеприпасов для всех заданных количеств городов $n_{i} \in N = {25, 50, 100, 250, 500}$ .
Визуализировать полученные результаты.

Города генерировать случайным образом с помощью равномерного распределения. При этом необходимо обеспечить возможность воспроизведения расчёта настройкой параметра seed у используемого генератора случайных чисел.

Размер пространства принять 100 на 100 км.

Important

Никаких других - «дополнительных», «удобных», «авторских» - условий в задаче не требуется.

Вариант 4 - Условная и безусловная оптимизация#

Цель - закрепить навыки численной оптимизации математических функций одного, двух и многих переменных.

Задача - рассмотреть и проанализировать способы (методы) оптимизации математических функций одного, двух и многих переменных.

Требуется оптимимизировать - т.е. найти значения аргументов, минимизирующих целевую функцию - следующие функции:

Функцию Бута:

(12)#

f (x, y) = (x + 2 y - 7)^{2} + (2 x + y - 5)^{2} .

Область определения аргументов: $- 10 \leq x, y \leq 10$ . Показать, что $f (1, 3) = 0$ есть минимум.

Функцию Розенброка от трёх параметров:

f (x_{1}, x_{2}, x_{3}) = \sum_{i = 1}^{2} [100 {(x_{i + 1} - x_{i}^{2})}^{2} + (x_{i} - 1)^{2}] .

Область определения аргументов: $- \infty \leq x_{1}, x_{2}, x_{3} \leq \infty$ . Показать, что $f (1, 1, 1) = 0$ есть минимум.

Функцию Экли:

(13)#

f (x, y) = - 20 \exp [- 0.2 \sqrt{\frac{x^{2} + y^{2}}{2}}] - \exp [\frac{\cos (2 π x) + \cos (2 π y)}{2}] + e + 20.

Область определения аргументов: $- 5 \leq x, y \leq 5$ . Показать, что $f (0, 0) = 0$ есть минимум.

Ограниченную функцию Мишры-Бёрда:

(14)#

f (x, y) = \sin (y) \exp [(1 - \cos x)^{2}] + \cos (x) \exp [(1 - \sin y)^{2}] + (x - y)^{2}

при ограничении

(x + 5)^{2} + (y + 5)^{2} < 25.

Область определения аргументов: $- 10 \leq x \leq 0$ и $- 6.5 \leq y \leq 0$ . Показать, что $f (- 3.1302468, - 1.5821422) = - 106.7645367$ есть минимум.

Постройте графики функций (12), (13) и (14).