Дискретно-событийное моделирование

Дискретно-событийное моделирование#

Дискретно-событийное моделирование (ДСМ) - это разновидность имитационного моделирования. Рассмотрим, как устроено ДСМ с использованием Python в контексте библиотеки SimPy, функциональности которой достаточно для создания сложных многоуровневых имитационных моделей со множеством агентов.

Начнём с рассмотрения основ SimPy. Затем рассмотрим простую и показательную задачку о движении материальной точки (шарика) в ограниченном двумерном пространстве (ящике, коробке). Затем подробнее рассмотрим некоторые примеры из документации SimPy.

Основы SimPy#

Для начала импортируем библиотеку:

import simpy as sim

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 import simpy as sim

ModuleNotFoundError: No module named 'simpy'

Подход ДСМ основан на понятии “событие”. При наступлении события должны быть выполнены те или иные действия, которые определяются создателями модели (нами). Это так называемая модель “событие - действие”. Чтобы её прояснить рассмотрим такой пример.

Пусть в некоторой нашей имитационной модели \(n\) событий следуют друг за другом через случайный промежуток времени \(\tau\). Пусть величина \(\tau\) распределена по экспоненциальному закону с плотностью вероятности

\[ \rho(\tau) = \cfrac{1}{\tau_{\rm mean}} \exp{\left( -\cfrac{\tau}{\tau_{\rm mean}} \right)}, \]

где \(\tau_{\rm mean}\) - средняя величина времени между событиями.

Тогда в коде это выражается следующим образом:

from numpy.random import default_rng

def exp_time(env, tau_mean, n, seed=None):
    """Генерирует события через случайные
    промежутки времени.

    env - объект среды SimPy.
    tau_mean - среднее время между событиями.
    n - количество событий.
    seed - затравка для генератора случайных чисел.
    """
    rg = default_rng(seed)
    for i in range(n):
        tau = rg.exponential(tau_mean)
        yield env.timeout(tau)
        print(f"Событие {i+1} наступило в {env.now}")

env = sim.Environment()
events_gen = exp_time(env, tau_mean=3., n=5)
env.process(events_gen)
env.run()

Событие 1 наступило в 0.9366925032480682
Событие 2 наступило в 7.582409661592764
Событие 3 наступило в 7.757931973981688
Событие 4 наступило в 8.226352505480024
Событие 5 наступило в 10.084292174730727

Что сделано:

  1. Для генерации случайных чисел импортировали функцию инициализации генератора по умолчанию.

  2. Описали генераторную функцию (см. раздел Генераторы) exp_time.

  3. Инициализировали среду SimPy sim.Environment и сохранили в переменной env. Именно в этот момент SimPy создаёт журнал событий, список процессов и т.д.

  4. Инициализировали, но не запустили (!), процесс методом env.process, передав ему генератор событий.

  5. Запустили ДСМ методом env.run.

В генераторной функции exp_time при её вызове:

  1. Инициализируется генератор случайных чисел.

  2. Поток выполнения программы входит в цикл for по числу событий n.

  3. Генерируется величина \(\tau\).

  4. Оператор yield возвращает генератор событий типа sim.Timeout. Поток выполнения возвращается в место вызова exp_time, в данном случае в строку events_gen = ....

При вызове функции exp_time создаётся генератор событий, сохраняемый в переменной events_gen. Далее events_gen передаётся в качестве аргумента методу env.process, регистрирующему SimPy-процесс. С этого момента env “знает” о существовании этого процесса. При вызове метода env.run SimPy “под капотом” запускает свой основной цикл или цикл обновления. Последовательность этого цикла в общих чертах следующая:

  1. Обходится список зарегистрированных генераторов событий - в нашем случае генератор всего один (результат вызова exp_time) и зарегистрирован он при вызове env.process. С каждым таким генератором ассоциировано событие, время наступления которого в нашем случае известно, но в общем случае может быть и неизвестным (см. пример в Ожидание события). В нашем случае событием является истечение времени ожидания env.timeout.

  2. Выбирается генератор с ближайшим событием (у нас он всего один). При этом обновляется счётчик глобального времени env.now и выполняется ряд других действий “под капотом”. К этому генератору применяется функция next - это и означает наступление события.

  3. Поток управления входит в генераторную функцию (exp_time) - выполняется код, расположенный под yield, пока не будет достигнут очередной оператор yield или функция exp_time не завершится. Это соответствует выполнению действий в ответ на событие.

  4. Цикл повторяется.

Никакой магии, никаких особенностей - чистый Python. Таким образом SimPy реализует концепцию ДСМ “событие - действие”. Далее рассмотрим более показательную задачу.

Шарик в коробке#

Представьте прямоугольную коробку, внутри которой от стенки к стенке движется шарик. Когда он достигает границы области, то упруго от неё отскакивает. Пусть пространство будет ограничено прямоугольником шириной \(w\) и высотой \(h\). Шарик в начальный момент времени \(t_0 = 0\) находится в случайной точке \((x_0, y_0)\) внутри прямоугольника и имеет случайную скорость \((v_x, v_y)\) постоянную по величине: \(v = \sqrt{v_x^2 + v_y^2} = \mathrm{const}\).

При абсолютно упругом ударе о вертикальные стенки отражается x-составляющая скорости \(v_x' = -v_x\), при ударе о горизонтальные - y-составляющая: \(v_y' = -v_y\).

Мы хотим промоделировать движение шарика в коробке в течение заданного времени \(T\). Как это сделать?

Одно из решений, часто первым приходящим на ум, заключается в задании некоторого постоянного малого шага по времени \(\Delta t\). Однако сразу возникает два вопроса:

  1. Как определить, какой шаг является малым, а какой - большим?

  2. Постоянная величина шага \(\Delta t\) приводит к проблеме пересечения границ, т.е. тело выходит за границы расчётной области и на деле ударяется не о стенку коробки, а о что-то, расположенное вне её. Это кардинально меняет траекторию тела, по сути нарушая условия задачи.

Шаг по времени в данной задаче зависит от размеров прямоугольника и скорости тела. Чем меньше область и больше скорость, тем меньше должен быть шаг \(\Delta t\). Скажем, при скорости 1 м/с и шаге по времени 0.1 с шарик выйдет за границу не более, чем на \(1 \cdot 0.5 = 0.1\) м. Если размеры прямоугольника составляют десятки и более метров, то погрешность в 0.1 м не велика. Однако тогда понадобится очень большое число промежуточных шагов, при которых никаких событий (столкновений) в системе не происходит. Компьютер тратит время впустую (и мы вместе с ним). Более того, методическая ошибка в расчёте столкновений всё же присутствует, сколь малой бы она ни была. Если за время моделирования шарик столкнётся со стенками 10 раз - мы получим одну величину ошибки \(\varepsilon_1\) в определении конечного положения тела. Если же столкновений будет 100000, то ошибка \(\varepsilon_2\) конечного положения будет много больше ошибки \(\varepsilon_1\). Следовательно, при итеративном подходе методическая ошибка расчёта накапливается. Ошибка накапливается также ввиду конечной точности представления вещественных чисел в компьютере.

Рассмотренный подход называется итеративным. Каждая итерация представляет из себя следующую последовательность действий:

  1. \(x_{i+1} = x_i + v_{x\, i+1} \Delta t_i\).

  2. \(y_{i+1} = y_i + v_{y\, i+1} \Delta t_i\).

  3. \(t_{i+1} = t_i + \Delta t_i\).

  4. Проверка пересечения границ. Если границы пересечены, то меняется знак соответствующей проекции скорости. Например, при столкновении с правой или левой стенкой \(v_{x\, i+1} = -v_{xi}\). Если столкновения нет, то проекции не изменяются: \(v_{x\, i+1} = v_{xi}\) и \(v_{y\, i+1} = v_{yi}\).

  5. Итерации повторяются, пока \(t_i < T\).

Проверка пересечения границ заключается в проверке условий \(x \notin (x_\mathrm{lb}; x_\mathrm{rb})\) и \(y \notin (y_\mathrm{bb}; y_\mathrm{tb})\), где \(x_\mathrm{lb}\) и \(x_\mathrm{rb}\) - прямые левой и правой границ соответственно; \(y_\mathrm{bb}\) и \(y_\mathrm{tb}\) - прямые нижней и верхней границ соответственно.

Если не спешить и обдумать задачу более основательно, то можно заметить, что по известной и постоянной скорости, начальному положению тела и при известных размерах пространства несложно рассчитать промежуток времени \(\Delta t_i\), через который тело столкнётся с одной из границ. Действительно, если в момент времени \(t_i\) проекции скорости тела \(v_{xi} > 0\) и \(v_{yi} > 0\), то шарик движется в направлении вправо вверх. Остаётся определить, какая из двух границ - правая или верхняя - будет достигнута быстрее. Если координата последнего столкновения шарика в момент времени \(t_i\) есть \((x_i, y_i)\), то с правой границей он столкнётся через время \(\Delta t_{\mathrm{rb} i} = (x_\mathrm{rb} - x_i) / v_{xi}\), а с верхней - через \(\Delta t_{\mathrm{tb} i} = (y_\mathrm{tb} - y_i) / v_{yi}\). И тогда \(t_{i+1} = t_i + \min(\Delta t_{\mathrm{rb} i}, \Delta t_{\mathrm{tb} i})\). Аналогично рассчитывается время столкновения с любой границей в зависимости от комбинации знаков проекций скорости тела.

Note

Если какая-либо из проекций равна нулю, то достаточно рассмотреть лишь одну границу, в направлении которой движется тело.

Таким образом, мы можем рассчитать момент времени \(t_{i+1}\) наступления следующего (\((i+1)\)-го) события “столкновение со стенкой”. Зная \(\Delta t_i\) и закон движения тела, мы можем точно рассчитать точку столкновения с границей: \(x_{i+1} = x_i + v_{xi} \Delta t_i\) и \(y_{i+1} = y_i + v_{yi}\Delta t_i\), после чего изменить знак соответствующей проекции скорости: либо \(v_{x\, i+1} = -v_{xi}\), либо \(v_{y\, i+1} = -v_{yi}\). После этого рассчитывается время до следующего столкновения и т.д.

При этом нам не нужно:

  • думать о выборе шага по времени - в реальных задачах от времени может зависеть большое число параметров, вследствие чего крайне затруднительно выбрать постоянный шаг по времени;

  • впустую тратить расчётное время компьютера - он обсчитает лишь моменты, в которых меняется состояние системы (в данном случае, когда при столкновении меняется знак у одной из проекций скорости);

  • знать сколько раз за время моделирования \(T\) шарик столкнётся со стенками.

При применении ДСМ методическая расчётная ошибка равна нулю и не накапливается. Получается траектория движения шарика, точно совпадающая с теоретической.

Important

Состояние системы изменяется при наступлении какого-либо события. Между событиями состояние остаётся постоянным. Это одно из основных положений ДСМ.

Для сравнения результатов реализуем и итеративный, и дискретно-событийный подходы.

Итеративный подход#

Напишем функцию итеративного решения задачи о шарике в коробке. Назовём её iterative_solver. Чтобы было легче воспринимать код, распределим его на функции.

import numpy as np


def iterative_solver(bounds, xy, v_xy, t_until, t_step):
    """Итеративный решатель задачи о шарике в коробке.
    
    * `bounds` - кортеж из 4 чисел, описывающих соответственно
      левую, правую, нижнюю и верхнюю границы прямоугольной области.
    * `xy` - начальная координата шара `(x, y)`.
    * `v_xy` - кортеж `(v_x, v_y)` со значениями проекций вектора
       начальной скорости точки.
    * `t_until` - время моделирования.
    * `t_step` - постоянный шаг по времени.
    """
    # Распакуем аргументы-кортежи в соответствующие переменные
    x, y = xy
    v_x, v_y = v_xy
    # Инициализируем "часы"
    t = 0
    # и массив траекторных точек
    # (именно эти три переменные формируют траекторию)
    traj = [(t, x, y)]
    # Выполняем итерации:
    while t <= t_until:
        # 1. Обновляем координаты и время
        x += v_x * t_step
        y += v_y * t_step
        t += t_step
        # 2. Проверяем условие столкновения
        flag, (sv_x, sv_y) = collision(bounds, (x, y))
        # 3. Инвертируем проекции скорости
        #    (если было столкновение)
        if flag:
            # Чтобы не расходавать память
            # на точки между столкновениями,
            # будем запоминать только точки столкновений
            traj.append((t, x, y))
            # Инвертируем проекции скорости
            v_x *= sv_x
            v_y *= sv_y
    # В завершение добавим последнюю точку траектории
    traj.append((t, x, y))
    # Возвращаем полученную траектории как массив NumPy
    return np.array(traj)


def collision(bounds, xy):
    """Условие столкновения шара с границами коробки.

    * `bounds` - кортеж четырёх элементов,
      хранящий координаты левой, правой, нижней и верхней границ
      прямоугольной области.
    * `xy` - текущая координата `(x, y)` шара.
    
    Возвращает кортеж из двух единичных значений, определяющих,
    нужно ли инвертировать соответствующую проекцию скорости.
    """
    x_lb, x_rb, y_bb, y_tb = bounds
    x, y = xy
    # Знак элемента signs показывает, нужно ли инвертировать
    # соответствующую проекцию скорости
    signs = [1, 1]
    # Флаг, показывающий было ли столкновение
    flag = False
    if not x_lb < x < x_rb:
        # Столкновение с одной из вертикальных стен,
        # значит, нужно инвертировать v_x
        signs[0] = -1
        flag = True
    if not y_bb < y < y_tb:
        # Столкновение с одной из горизонтальных стен,
        # значит, нужно инвертировать v_y
        signs[1] = -1
        flag = True
    return flag, signs

Функция collision проверяет условия столкновения, которые, напомним, имеют следующий вид:

\[ x_i \notin (x_\mathrm{lb}; x_\mathrm{rb}), \quad y_i \notin (y_\mathrm{bb}; y_\mathrm{tb}). \]

Warning

Функция collision имеет один эффект, влияющий на траекторию шара, который мы не предусмотрели. Получится ли у вас его определить?

Опишем удобную для многоразового использования функцию визуализации траектории plot_traj:

import matplotlib.pyplot as plt


def plot_traj(traj, figax=None, **kw):
    """Строит траекторию тела.
    
    * `traj` - прямоугольная матрица, каждая строка
      которой соответствует точке траектории. Точка траектории
      описывается тремя величинами: временем столкновения
      и x- и y-координатой точки в этот момент.
    * `figax` - кортеж двух элементов: рисунка и оси графика.
    """
    if figax is None:
        fig, ax = plt.subplots()
    else:
        fig, ax = figax
    # Линии траектории
    ax.plot(traj[:, 1], traj[:, 2], **kw)
    # Начальная и конечная точки
    ax.plot(traj[0, 1], traj[0, 2],
            ls="", marker="o", c="purple")
    ax.plot(traj[-1, 1], traj[-1, 2],
            ls="", marker="x", c="purple")
    return fig, ax

Посмотрим, что получилось. Пусть условия задачи таковы (единицы измерения нас не интересуют):

  • \(x_\mathrm{lb} = 0\), \(x_\mathrm{rb} = 1\), \(y_\mathrm{bb} = 0\) и \(y_\mathrm{tb} = 1\);

  • \(x_0 = 2/3\) и \(y_0 = 1/3\);

  • \(v_{x0} = 0.3\) и \(v_{y0} = 0.1\);

  • шаг по времени \(\Delta t = 0.5\);

  • время моделирования \(T = 60\).

# Условия задачи
bounds = 0, 1, 0, 1
xy = 0.67, 0.33
v = 0.3, 0.1
dt = 0.5
t_until = 60

Моделируем и строим траекторию:

traj = iterative_solver(bounds, xy, v, t_until, dt)
_, ax = plot_traj(traj)
ax.axvline(bounds[0], color="k")
ax.axvline(bounds[1], color="k")
ax.axhline(bounds[2], color="k")
ax.axhline(bounds[3], color="k")
ax.set(xlabel="$x$, м", ylabel="$y$, м", aspect="equal");
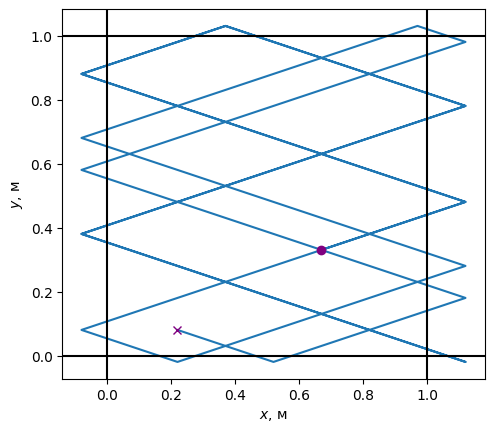
../_images/cd02002c1b2ec62ee4d81e448a97028267a42ddf818c863d92c10b236be9d96a.png

Число столкновений:

print("Число столкновений:", traj.shape[0] - 1)
# Не учитывая последнюю (свободную) точку

Число столкновений: 21

Note

Кстати, о непредусмотренном эффекте функции collision. Этот эффект виден на получившемся графике. Постарайтесь его найти и объяснить.

Если уменьшить шаг по времени в 5 раз, то получим следующую картину:

traj_iterative = iterative_solver(
    bounds, xy, v, t_until, t_step=dt/5
)
_, ax = plot_traj(traj_iterative)
ax.axvline(bounds[0], color="k")
ax.axvline(bounds[1], color="k")
ax.axhline(bounds[2], color="k")
ax.axhline(bounds[3], color="k")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
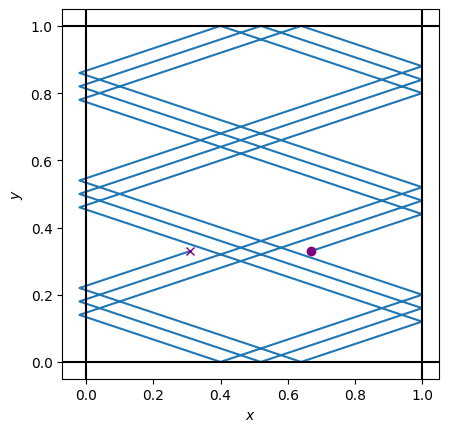
../_images/63621037c080c9bac205f5f731df5dc9dc5cbab71d116ee8692998d92f3e2f48.png 
print("Число столкновений:", traj_iterative.shape[0] - 1)

Число столкновений: 25

Сравнив два рисунка, можно заметить, что хоть уменьшение шага и привело к более точной траектории тела, но пересечение границ всё равно присутствует. Также при различном временном шаге получены разные значения числа столкновений: 21 и 25 соответственно.

Note

Заметьте, что столкновение с горизонтальными границами происходит почти на них. На самом деле при данном масштабе не видно, что выход за границу по вертикальной оси составляет 0.03 м. Можно и так подобрать параметры задачи (шаг по времени, скорость и начальную координату шара), что столкновение будет происходить точно на границах. Но это будет либо совпадением, либо подгонкой параметров, которую бывает невозможно произвести в сложных задачах.

Настало время решить эту задачу правильно.

Дискретно-событийный подход#

Как отмечено выше, при дискретно-событийном подходе мы должны рассчитать момент наступления события.

def de_solver(bounds, xy, v_xy, t_until):
    """Решатель, рализующий подход ДСМ.
    
    * `bounds` - кортеж из 4 чисел, описывающих соответственно
      левую, правую, нижнюю и верхнюю границы прямоугольной области.
    * `xy` - начальная координата шара `(x, y)`.
    * `v_xy` - кортеж `(v_x, v_y)` со значениями проекций вектора
       начальной скорости точки.
    * `t_until` - время моделирования.
    """
    # Для удобства расчётов сделаем NumPy-массивы
    xy, v_xy = np.array(xy), np.array(v_xy)
    # Инициализируем SimPy-среду.
    env = sim.Environment()
    # Сохраним начальную точку траектории
    traj = [(env.now, *xy)]
    # Регистируем процесс motion
    env.process(motion(env, bounds, xy, v_xy, traj))
    # Запускаем моделирование в течение заданного времени
    env.run(until=t_until)
    # Сохраним точку траектории в конце моделирования
    xy += v_xy * (t_until - traj[-1][0])
    traj.append((env.now, *xy))
    # Возвращаем траекторию в виде NumPy-массива
    return np.array(traj)


def motion(env, bounds, xy, v_xy, traj):
    """Генераторная функция для событий столкновения с границами.
    
    * `env` - объект среды SimPy.
    * `bounds` - кортеж из 4 чисел, описывающих соответственно
      левую, правую, нижнюю и верхнюю границы прямоугольной области.
    * `xy` - координата последнего столкновения тела.
    * `v_xy` - скорость тела после последнего столкновения.
    * `traj` - прямоугольная матрица, каждая строка
      которой соответствует точке траектории. Точка траектории
      описывается тремя величинами: временем столкновения
      и x- и y-координатой точки в этот момент.
    """
    while True:
        dt, signs = calc_delay(bounds, v_xy, xy)
        yield env.timeout(dt)
        xy += v_xy * dt
        traj.append((env.now, *xy))
        v_xy *= signs


def calc_delay(bounds, v_xy, xy):
    """Рассчитать величину времени, через которое наступит
    следующее событие, по заданным границам `bounds`,
    скорости шара `v_xy` и координате его последнего
    столкновения `xy`."""
    # Распакуем аргументы для удобства
    x_lb, x_rb, y_bb, y_tb = bounds
    x, y = xy
    vx, vy = v_xy
    # Вычисляем время (задержку):
    dtx, dty = 0., 0.
    # - в направлении оси Ox
    if vx > 0:
        dtx = (x_rb - x) / vx
    elif vx < 0:
        dtx = (x_lb - x) / vx
    # - в направление оси Oy
    if vy > 0:
        dty = (y_tb - y) / vy
    elif vy < 0:
        dty = (y_bb - y) / vy
    # Определяем, какую проекцию скорости инвертировать
    signs = [1, 1]
    signs[np.argmin((dtx, dty))] = -1
    return min(dtx, dty), signs

Сформированная программа с точки зрения ДСМ ничем не отличается от программы в примере из раздела Основы SimPy. Разница лишь в том, что в данном случае время между событиями мы рассчитываем (в функции calc_delay), а не генерируем как случайное число.

Промоделируем при тех же условиях:

# Заметьте, мы уже не задаём шаг по времени
traj_des = de_solver(bounds, xy, v, t_until)
_, ax = plot_traj(traj_des)
ax.axvline(bounds[0], color="k")
ax.axvline(bounds[1], color="k")
ax.axhline(bounds[2], color="k")
ax.axhline(bounds[3], color="k")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
print("Число столкновений:", traj_des.shape[0] - 1)

Число столкновений: 25
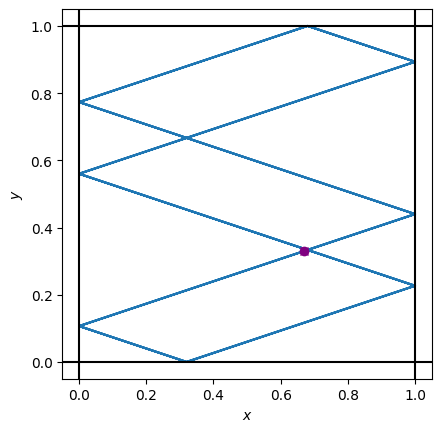
../_images/22a53799da0707dd19aebd92d018031b32b318d5197e4a3a35c32d12668768cb.png

Получили точное решение, которое заметно отличается от всех решений, полученных ранее - шарик оказался в том же самом месте, из которого начал своё движение.

Итак, приведём полученные результаты на одном графике:

fig, ax = plot_traj(traj_iterative, label="Итеративный метод")
plot_traj(traj_des, (fig, ax), label="ДСМ")
ax.legend(loc="upper right")

ax.axvline(bounds[0], color="k")
ax.axvline(bounds[1], color="k")
ax.axhline(bounds[2], color="k")
ax.axhline(bounds[3], color="k")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
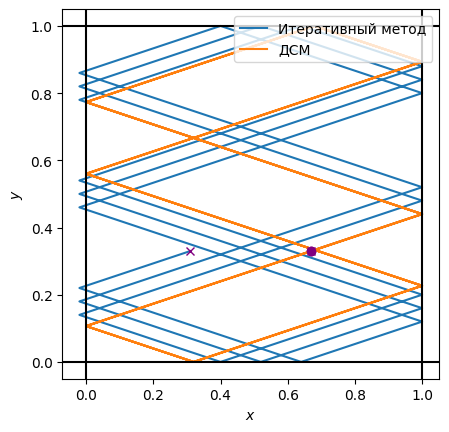
../_images/b19ac6f0ab6228795143cb105a18aeed82b91493dfbc3ad2e7d0f96d29d5af37.png

Из полученного графика также отчётливо видно, как по мере увеличения числа событий, увеличивается ошибка итеративного метода. С течением времени полученная с его помощью траектория всё сильнее и сильнее отклоняется от теоретической (оранжевой). В данном случае относительная ошибка в определении конечного положения составляет примерно 40% (!).

Изменим начальные условия и посмотрим на результат:

# Немного другие условия задачи
bounds = 0, 2, 0, 1
xy = 0.6, 0.2
v = 0.3, -0.1
t_until = 40    # ...равно периоду движения

traj = de_solver(bounds, xy, v, t_until)

# Показываем
_, ax = plot_traj(traj)
ax.axvline(bounds[0], color="k")
ax.axvline(bounds[1], color="k")
ax.axhline(bounds[2], color="k")
ax.axhline(bounds[3], color="k")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
print("Число столкновений:", traj.shape[0] - 1)

Число столкновений: 11
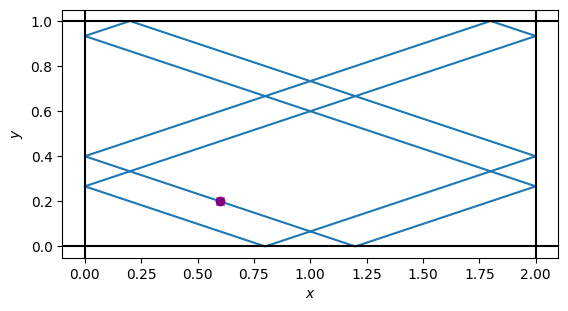
../_images/f450c0fd2be1ad4d28df5927c77ffa041e45ce25504e06abba1a7e837e5e2ca7.png

Note

Интересно подумать, почему получается периодическое движение и как рассчитать его период?

Для дальнейшего изучения SimPy достаточно отличной официальной документации с примерами

Примеры использования SimPy#

В данном разделе рассмотрены некоторые примеры из официальной документации SimPy с целью чуть лучше раскрыть принципы работы с данной библиотекой.

Прежде необходимо подключить SimPy:

import simpy as sim

Разочарование клиента в банке#

Данный пример раскрывает такие возможности SimPy, как ресурсы и условные события.

Задача следующая. Есть банк, в который приходят клиенты. У банка есть несколько окон для обслуживания клиентов. Поток клиентов случаен. Каждый клиент имеет определённое терпение, которое может закончиться, и клиент в результате просто уйдёт из банка. Если же его очередь подойдёт быстрее, чем закончится терпение, то он подойдёт к окну и займёт его на некоторое время. Остальные клиенты всё так же продолжат ждать своей очереди, насколько хватит терпения.

Нам точно понадобится рандом:

import random as rand

Также задаём основные параметры модели:

RANDOM_SEED = 42
NEW_CUSTOMERS = 5  # Общее число посетителей
INTERVAL_CUSTOMERS = 10.0  # Среднее время появления нового посетителя
MIN_PATIENCE = 1  # Минимальное
MAX_PATIENCE = 3  # и максимальное время ожидания клиента

Определим клиента как функцию-процесс (в терминах SimPy) customer. По сути своей, это обычная генераторная функция.

def customer(env, name, counter, time_in_bank):
    """Посетитель приходит, обслуживается и уходит."""
    arrive = env.now
    print(f"{arrive:7.4f} {name}: Я пришёл!")
    # Клиент "запрашивает" обслуживание, т.е. ресурс в терминах SimPy.
    # counter - это сотрудник банка (окно обслуживания).
    with counter.request() as req:
        # Каково же терпение!
        patience = rand.uniform(MIN_PATIENCE, MAX_PATIENCE)
        # Ожидание своей очереди, пока хватает терпения.
        # Это и есть условное событие: либо пришла очередь,
        # либо кончилось терпение. Оператор ИЛИ в yield-выражении
        # обозначается вертикальной чертой "|", как побитовое ИЛИ.
        results = yield req | env.timeout(patience)
        # Отмечаем, сколько клиент прождал
        wait = env.now - arrive
        # В results у нас список НАСТУПИВШИХ событий.
        # В данном случае могло наступить всего одно событие:
        # либо req, либо истекло время ожидания (timeout).
        if req in results:
            # Освободился ресурс (окно) - настала очередь клиента
            print(f"{env.now:7.4f} {name}: Прождал {wait:6.3f}")
            # Теперь клиент на случайное время занимает окно.
            # Всё это время ресурс req занят и не доступен
            # другим посетителям.
            tib = rand.expovariate(1.0 / time_in_bank)
            yield env.timeout(tib)
            print(f"{env.now:7.4f} {name}: Довольный ухожу")
        else:
            # Кончилось терпение!
            print(f"{env.now:7.4f} {name}: УХОЖУ после ожидания {wait:6.3f}!")

Теперь опишем генераторную функцию, ответственную за возникновение новых посетителей. Назовём её source. Она будет процессом в терминах SimPy.

def source(env, number, interval, counter):
    """Случайным образом генерирует посетителей."""
    for i in range(number):
        c = customer(
            env,
            f"Посетитель с талончиком {i+1}",
            counter,
            time_in_bank=12.0
        )
        env.process(c)
        # Через сколько этот клиент нагрянет в банк?
        t = rand.expovariate(1.0 / interval)
        # Генерируем событие "Новый посетитель"
        yield env.timeout(t)

Теперь можно и моделировать:

# Настраиваем и запускаем симуляцию
print("Банковская идилия")
rand.seed(RANDOM_SEED)
env = sim.Environment()
# Запускаем процессы и прогонку (run) модели.
# - Окно обслуживания у нас всего одно и оно является ресурсом
#   в терминах SimPy.
counter = sim.Resource(env, capacity=1)
# - Инициализируем процесс появления клиентов, который, в свою очередь,
#   генерирует посетителя, запускает его как процесс, а потом ждёт,
#   прежде чем сгенерировать нового клиента.
env.process(source(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter))
# - Так как всего будет NEW_CUSTOMERS посетителей, то симуляция
#   сама собой завершится, когда уйдёт последний клиент.
#   Поэтому нет нужды указывать run время моделирования until.
env.run()

Банковская идилия
 0.0000 Посетитель с талончиком 1: Я пришёл!
 0.0000 Посетитель с талончиком 1: Прождал  0.000
 3.8595 Посетитель с талончиком 1: Довольный ухожу
10.2006 Посетитель с талончиком 2: Я пришёл!
10.2006 Посетитель с талончиком 2: Прождал  0.000
12.7265 Посетитель с талончиком 3: Я пришёл!
13.9003 Посетитель с талончиком 3: УХОЖУ после ожидания  1.174!
23.7507 Посетитель с талончиком 2: Довольный ухожу
34.9993 Посетитель с талончиком 4: Я пришёл!
34.9993 Посетитель с талончиком 4: Прождал  0.000
37.9599 Посетитель с талончиком 4: Довольный ухожу
40.4798 Посетитель с талончиком 5: Я пришёл!
40.4798 Посетитель с талончиком 5: Прождал  0.000
43.1401 Посетитель с талончиком 5: Довольный ухожу

Вот и результат. Не повезло лишь третьему талончику… Ну и банку тоже! Вдруг именно этим клиентом был Илон Маск?

Note

Кстати, сравните полученный результат с результатом официального примера. Абсолютно точное совпадение! Всё из-за того, что использовалась одна и та же затравка SEED для генератора псевдослучайных чисел. Ну и сам генератор был тем же самым - из стандартной библиотеки random.

Как видите, довольно просто и быстро можно смоделировать вполне реальную задачу из теории массового обслуживания. Ведь никто не мешает учесть здесь финансовую сторону вопроса и прийти к оптимизационной задачи по типу: “Сколько нужно обслуживающих окон, чтобы минимизировать потерю клиентов, т.е. максимизировать прибыль? Сколько нужно окон утром во вторник и вечером пятницы? Как при этом минимизировать затраты на новых сотрудников, но не ухудшить обслуживание? Поставить автоматы самообслуживания? Сколько их нужно? Когда и сколько денег в них загружать?” Ну вы поняли…

Important

Создаётся впечатление, будто процессы source и customer выполняются параллельно. На самом деле это не совсем так.

С точки зрения операционной системы поток выполнения нашей программы один, т.е. программа не “выполняется на нескольких ядрах”. Выражаясь технически, параллелизма на аппаратном уровне здесь нет. Но есть параллелизм на уровне программы.

У нас может быть любое количество запущенных процессов, но каждый процесс - это генератор.

Ожидание события#

…

Contents