Визуализация трёхмерных данных с использованием matplotlib#
Рассматриваются основы создания как трёхмерных графиков, так и двухмерных графиков для визуализации трёхмерных данных.
Создание трёхмерных осей#
Импортируем модуль pyplot:
import matplotlib.pyplot as plt
И создаём трёхмерные оси. Для этого сначала создаём объект окна fig класса plt.figure,
а затем методом fig.add_subplot(...) добавляем к нему ось с ключевым параметром projection="3d":
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
Далее с объектом ax можем выполнять все те же операции, что рассматрены в Основы построения графиков и Особенности matplotlib.
Attention
Создавать трёхмерные графики имеет смысл тогда и только тогда, когда они будут использоваться в интерактивном режиме, т.е. тогда, когда имеется возможность “вертеть” эти графики, рассматривая их со всех сторон и масштабируя.
Не стоит вставлять изображения трёхмерных графиков в бумажные отчёты!
Построим график такой функции:
в пределах \(x \in [-6, 6]\) и \(y \in [-6, 6]\).
Инициализация данных для визуализации#
Импортируем numpy и опишем функцию \(f(x, y)\):
import numpy as np
def f_sin_xy(x, y):
return np.sin(np.sqrt(x**2 + y**2))
Расчётная сетка#
Чтобы построить трёхмерный график, необходимо определить каждую пару \((x_i; y_j)\) (комбинацию из двух элементов массивов x и y), где \(i = 1, 2, \dots, N_x\) и \(j = 1, 2, \dots, N_y\). Другими словами, нам нужны точки \((x_1; y_1)\), \((x_1; y_2)\), \(\dots\), \((x_1; y_{N_y})\), \((x_2; y_1)\), \((x_2; y_2)\), \(\dots\), \((x_{N_x}; y_{N_y})\).
Для начала инициализируем два соответствующих массива x и y в оговорённых пределах по 51 значению в каждом:
x = np.linspace(-6, 6, 51) # N_x = 51
y = np.linspace(-6, 6, 51) # N_y = 51
Чтобы их массивов x и y сформировать расчётную сетку \((x_i; y_j)\), применим функцию numpy.meshgrid(...):
x, y = np.meshgrid(x, y)
Мы получим расчётную сетку размером \(N_x \times N_y\). Убеждаемся:
x.shape
(51, 51)
y.shape
(51, 51)
Important
Массивы x и y с этого момента имеют одинаковую форму даже в случае, если бы \(N_x \neq N_y\).
Теперь мы можем вычислить массив z значений функции \(f(x, y)\):
z = f_sin_xy(x, y)
z.shape
(51, 51)
Как видим, массив z имеет такую же форму, как и массивы x и y - функция вычислена в каждой точке.
Перейдём к способам визуализации.
Виды трёхмерных графиков#
Контурный график#
Есть три типа контурных графиков:
в виде линий уровня,
в виде заполненных цветом промежутков между линиями уровня и
их комбинация.
Линии уровня#
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.contour3D(x, y, z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
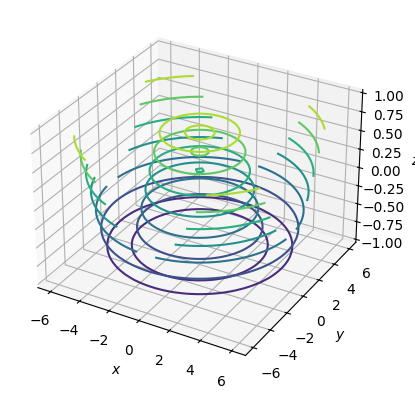
Линий уровня на рисунке выше маловато. Увеличим их число до 30:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.contour3D(x, y, z, levels=30)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
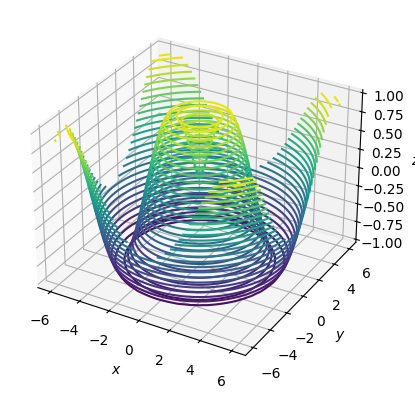
Note
Цвет в данном случае определяется значением координаты z.
Стоит отметить, что общий стиль графиков также можно изменять с помощью стилевого контекста:
with plt.style.context("bmh"):
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.contour3D(x, y, z, levels=30)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$")
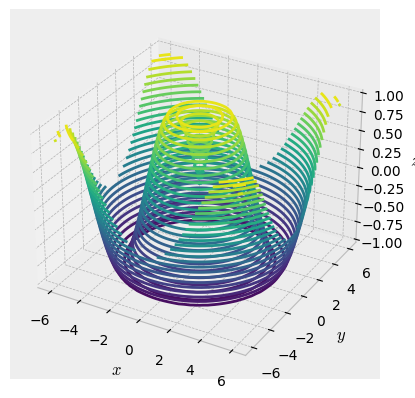
Заполненные контуры#
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.contourf3D(x, y, z, levels=30) # Буква "f" добавилась к названию "contour"
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
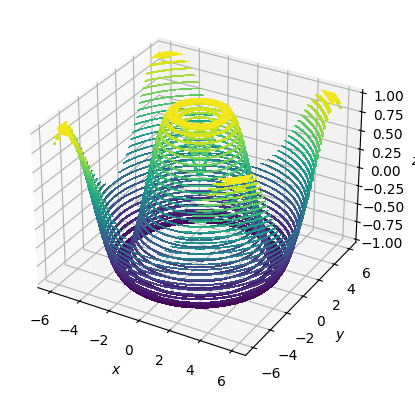
Attention
Не стоит применять такой график.
Каркас#
Представляет из себя набор прямых, соединяющих ближайшие соседние точки:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_wireframe(x, y, z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
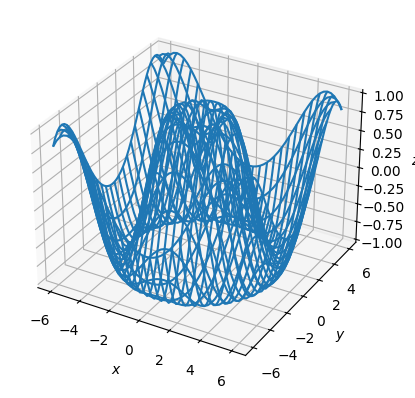
Поверхностный график#
Представляет собой заполненные цветом плоскости, образованные ближайшими соседними точками, т.е. области, ограниченные рёбрами каркасного графика:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_surface(x, y, z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
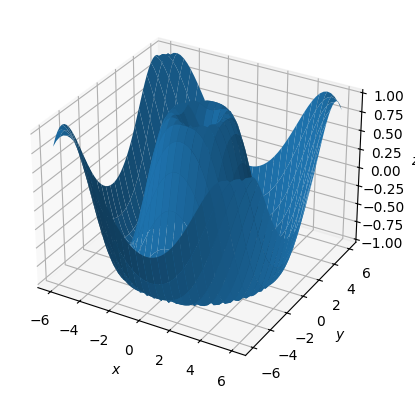
Можно задать конкретный цвет графика через параметр color или c:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_surface(x, y, z, color="green")
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
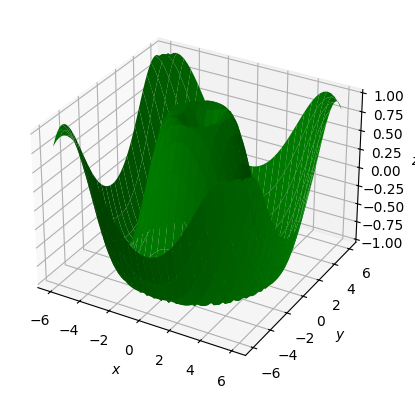
Или задать цветовую схему cmap (color map), например viridis.
Тогда цвет будет показывать относительную величину z-координаты.
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_surface(x, y, z, cmap="viridis")
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
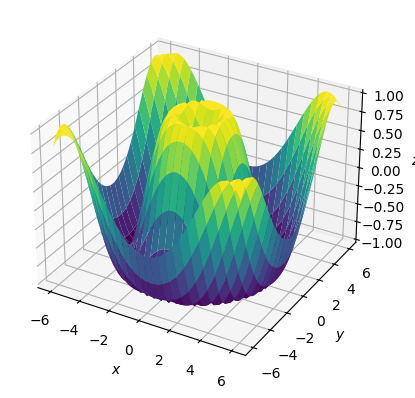
Точечный график#
Изобразим трёхмерные точки:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.scatter3D(x, y, z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
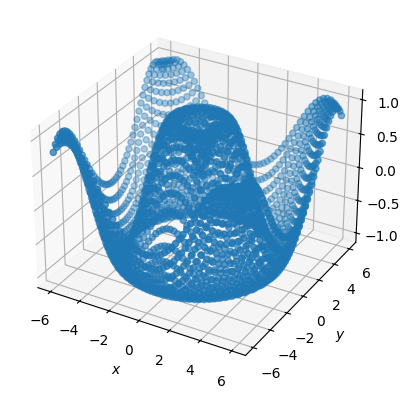
Можно поставить цвет точки в зависимость от значений той или иной координаты графика.
Это делается через параметр цвета c, которому присваивается желаемый массив, например, z:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.scatter3D(x, y, z, c=z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
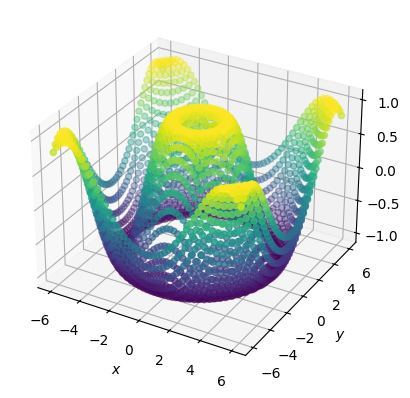
Или свяжем цвет с координатой x:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.scatter3D(x, y, z, c=x)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
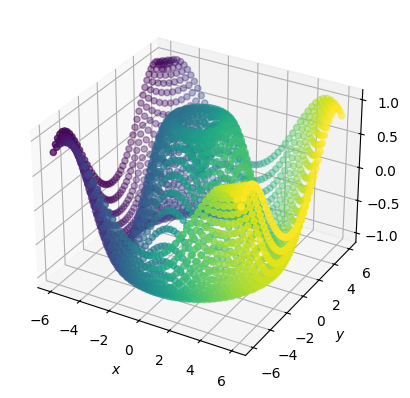
Или, и вовсе, сделаем выражением \((x - y)^2\):
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.scatter3D(x, y, z, c=(x-y)**2)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
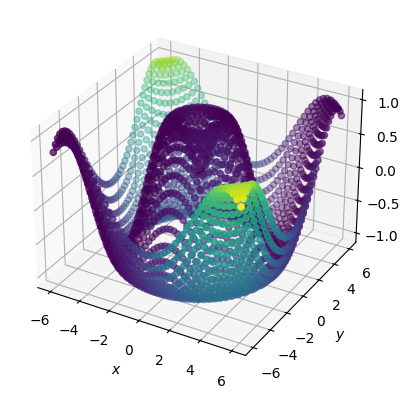
Attention
У данного типа графика (scatter3D) нет параметра color, только c.
Триангулированная поверхность#
Данный тип графиков несколько особенный.
Это объясняется его предназначением - таким способом строят сложные поверхности с неравномерной сеткой.
Примером такой поверхности может быть сфера, тор и т.п.
То есть точки для данного графика могут быть расположены в пространстве произвольным образом и на вход должны подаваться в виде одномерных массивов x, y, z.
Переиницилизируем массивы x и y, причём заполним их случайными значениями, и пересчитаем массив z:
x = np.random.uniform(-6, 6, 1001)
y = np.random.uniform(-6, 6, 1001)
z = f_sin_xy(x, y)
x.shape, y.shape, z.shape
((1001,), (1001,), (1001,))
Убедимся, что эти точки расположены в пространстве хаотично, построив точечный график:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.scatter3D(x, y, z, c=z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
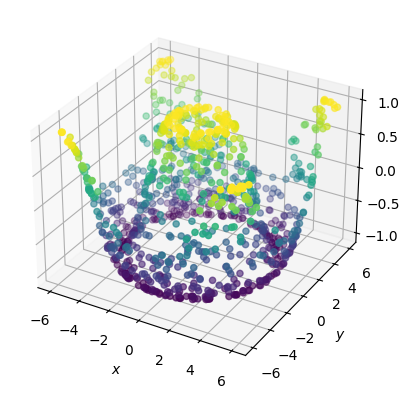
Очевидно, что точки действительно расположены в плоскости \(Oxy\) случайным образом.
Теперь построим триангулированную поверхность:
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_trisurf(x, y, z)
ax.set(xlabel="$x$", ylabel="$y$", zlabel="$z$");
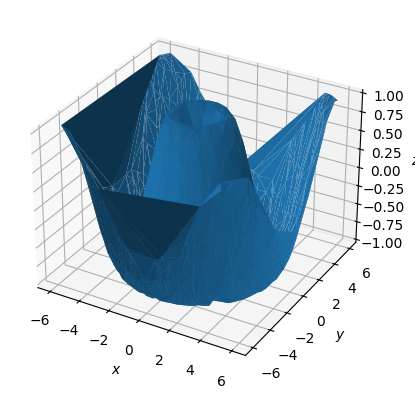
Триангулированные поверхности строятся как выпуклые оболочки, этим и достигается возможность однозначного связывания точек.
Note
Очевидно, что поверхность будет тем качественнее, чем большее количество точек задано.
Important
К настоящему моменту после просмотра ряда неинтерактивных трёхмерных графиков должно сформироваться понимание их малой информативности и ценности при использовании в бумажных (плоских) отчётах. Поэтому далее рассмотрим двумерные способы визуализации трёхмерных данных.
Стоит отметить, что возможно строить и трёхмерные кривые (и прямые), а также плоские кривые и точки, лежащие в одной плоскости, в трёхмерных осях.
Двухмерные способы визуализации трёхмерных данных#
Будем визуализировать всё ту же функцию \(f(x, y) = \sqrt{x^2 + y^2}\).
Актуализируем массивы x, y, z:
x, y = np.meshgrid(
np.linspace(-6, 6, 51),
np.linspace(-6, 6, 51)
)
z = f_sin_xy(x, y)
Как видите, массивы инициализированы абсолютно так же, как и для построения трёхмерных графиков. В общем и целом, методы построения графиков двухмерных визуализаций 3D-данных те же, что описаны выше.
Линии уровня#
Метод plt.axis.contour(...) построит нам линии уровня, как если бы мы смотрели на 3D-график сверху:
fig, ax = plt.subplots()
ax.contour(x, y, z, levels=30)
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
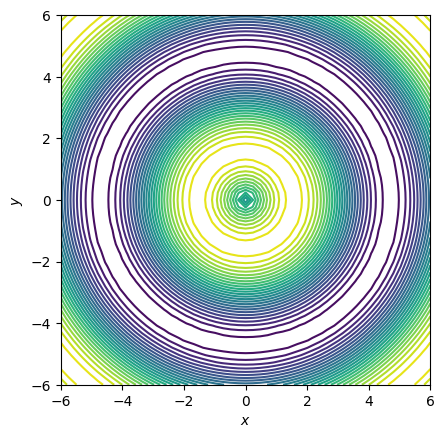
Однако по сравнению с 3D-графиками у нас явно остутствует третья ось - z.
Это приводит к тому, что не ясны значения цветов - видно лишь качественное поведение графика, но не видны абсолютные значения z, стоящие за ним. Исправить ситуацию поможет цветовая шкала (colorbar):
fig, ax = plt.subplots()
# Сохраняем изображение оси:
# именно на этом этапе цвета cmap связываются с данными z
image = ax.contour(x, y, z, levels=30)
# Используем это изображение для цветовой шкалы.
# Заодно присвоем шкале метку недостающей оси z
fig.colorbar(image, ax=ax, label="$z$")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
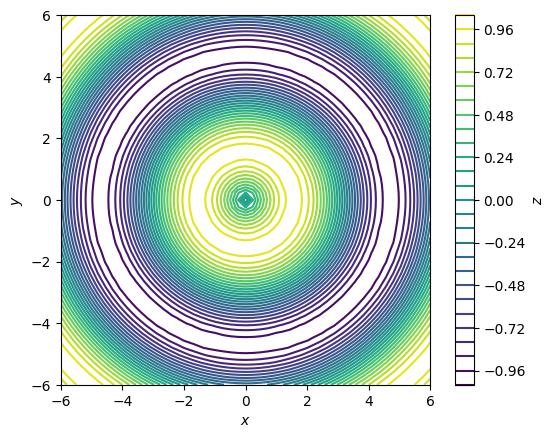
Вместо цветовой шкалы можно применить и другой подход - показывать абсолютные значения z прямо на линиях уровня (только число линий уровня нужно сделать небольшим):
fig, ax = plt.subplots()
# Сохраняем связь контуров с цветовой схемой
contours = ax.contour(x, y, z)
# и используем для инициализации меток в этих контурах
ax.clabel(contours, inline=True)
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
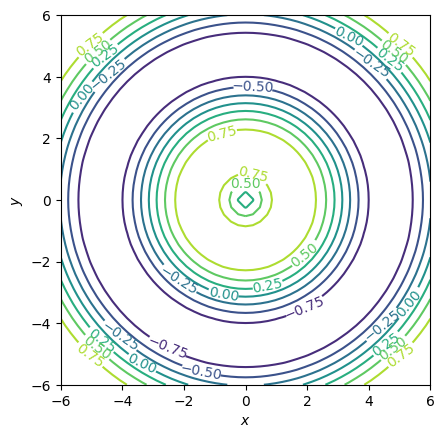
Заполненные контуры#
Аналогично contourf3D(...) функция plt.axis.contourf(...) строит линии уровня, линейно заполняя цветом пространство между ними. Для разнообразия используем стиль dark_background:
fig, ax = plt.subplots()
ax.contourf(x, y, z, levels=30)
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
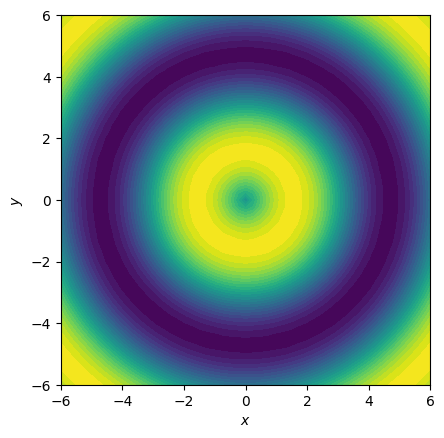
В данном случае так же не хватает значений третьей оси. Добавим цветовую шкалу:
fig, ax = plt.subplots()
contours = ax.contourf(x, y, z, levels=30)
fig.colorbar(contours, ax=ax, label="$z$")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
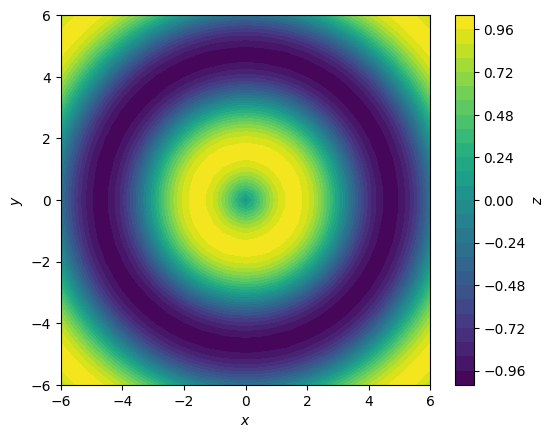
Заполненный контур с линиями уровня#
Для этого достаточно построить заполненный контур, а затем построить линии уровня.
Главное, чтобы линии уровня хорошо выделялись на фоне цветов заполненного контура.
Для этого сделаем линии уровня красными (cmap="Reds"):
fig, ax = plt.subplots()
# Строим заполненный контур
contours = ax.contourf(x, y, z, levels=30)
# и связанную с ним цветовую шкалу.
fig.colorbar(contours, ax=ax, label="$z$")
# Строим красные линии уровня
contours = ax.contour(x, y, z, levels=5, cmap="Reds")
# с метками значений на линии.
ax.clabel(contours, inline=True)
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
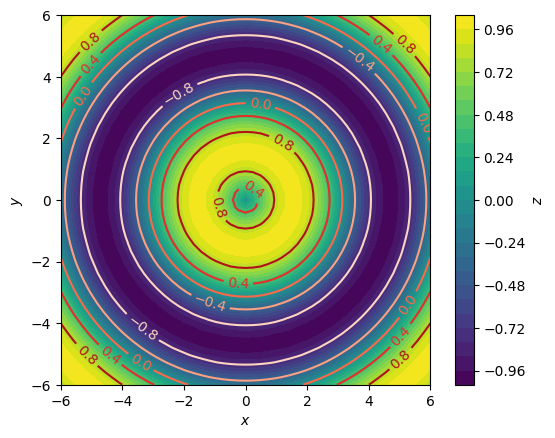
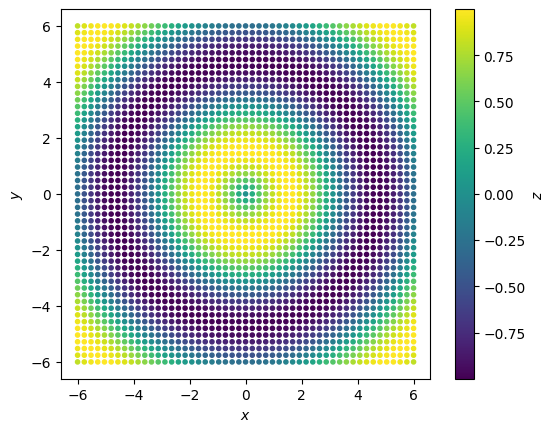
График разброса (точечный)#
Аналогичную функции plt.axis.scatter3D(...) работу выполняет метод plt.axis.scatter(...):
fig, ax = plt.subplots()
# Обратите внимание, что z не передаётся как координата,
# вместо этого z имеет смысл для инициализации цвета
points = ax.scatter(x, y, c=z, marker=".")
fig.colorbar(points, ax=ax, label="$z$")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
Создадим случайные массивы x и y и пересчитаем z:
x = np.random.uniform(-6, 6, 1001)
y = np.random.uniform(-6, 6, 1001)
z = f_sin_xy(x, y)
Снова построим график разброса:
fig, ax = plt.subplots()
points = ax.scatter(x, y, c=z, marker=".")
fig.colorbar(points, ax=ax, label="$z$")
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal");
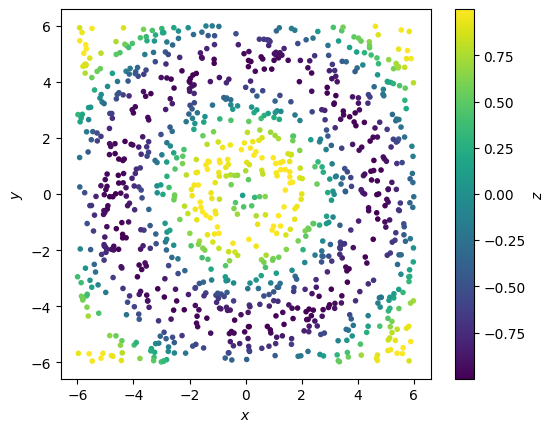
Удобство и информативность двумерных графиков трёхмерных данных очевидна.
Important
Используйте двумерные способы визуализации трёхмерных данных при оформлении бумажных отчётов по своим работам. Трёхмерную визуализацию оставьте для интерактивных способов публикации своих результатов.
