Мультипольное разложение в теории электромагнитного поля

В процессе выполнения данной задачи мы рассмотрим электростатический потенциал системы электрических зарядов, введя так называемое мультипольное разложение, которое позволит описывать задачу всего лишь небольшим набором чисел и получать при этом решение, хорошо согласующееся с реальными физическими свойствами. Такой подход подходит не только для потенциала Кулона, но и для гравитационного потенциала Ньютона.

На примере этой задачи рассмотрим сходимость рядов и рекурентных соотношений. Начнём с визуализации электрического поля системы множества зарядов по аналогии с Визуализация векторного поля. Далее выполним мультипольное разложение, используя полиномы Лежандра. В конце сформируем полноценный модуль Python для решения подобных задач, который будем использовать в последующих задачах.

Потенциал системы распределённых зарядов

Общий случай

Как должно быть известно из курса физики, ротор электрического поля \(\mathbf{E}(\mathbf{r})\) в любой точке \(\mathbf{r}\) пространства равен нулю. Следовательно, существует некая скалярная функция \(\varphi(\mathbf{r})\), именуемая электростатическим потенциалом, градиент которой и есть электрическое поле (ротор градиента всегда равен нулю):

(6)\[ \mathbf{E}(\mathbf{r}) = -\nabla \varphi(\mathbf{r}) = -\mathbf{grad}{\varphi(\mathbf{r})}, \]

где \(\nabla\) - векторный дифференциальный оператор, который в случае трёхмерного пространства имеет следующий вид:

\[ \nabla = \frac{\partial}{\partial x} \mathbf{i} + \frac{\partial}{\partial y} \mathbf{j} + \frac{\partial}{\partial z} \mathbf{k}, \]

где \(\mathbf{i}\), \(\mathbf{j}\), \(\mathbf{k}\) - базисные векторы.

Important

Знак “минус” в формуле (6) означает, что в направлении роста потенциала поля (градиент положителен) электрическое поле положительного заряда уменьшается. Это логично, учитывая физический смысл потенциала: \(\varphi\) - это работа электрического поля по перемещению заряда на бесконечное расстояние, где поле отсутствует. Соответственно, поле, создаваемое положительным зарядом \(+q\), совершает положительную работу при перемещении на бесконечность положительного тестового заряда \(+Q\), при этом величина поля с расстоянием убывает. Вот в чём “природа” минуса в (6).

Important

Знак потенциала \(\varphi\) зависит от знака тестового заряда \(Q\). Важно помнить о правиле знаков: \(\varphi > 0\) при \(Q > 0\) и \(\varphi < 0\) при \(Q < 0\).

Электростатический потенциал точечного (положительного) заряда \(q_0\) в некоторой точке пространства с радиус-вектором \(\mathbf{r}\) определяется по формуле:

\[ \varphi_0(\mathbf{r}) = k \cfrac{q_0}{\| \mathbf{r} - \mathbf{r}_0 \|}. \]

Несложно убедиться, что для потенциала системы \(n\) зарядов так же, как и для поля, справедлив принцип суперпозиции:

\[ \varphi(\mathbf{r}) = \sum\limits_{i=0}^{n-1}{\varphi_i(\mathbf{r})} = \sum\limits_{i=0}^{n-1}{k \cfrac{q_i}{\| \mathbf{r} - \mathbf{r}_i \|}}. \]

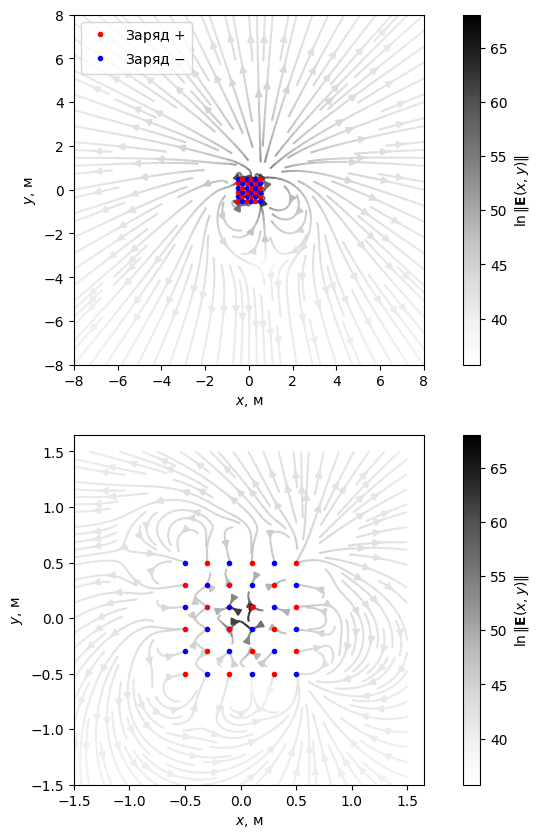
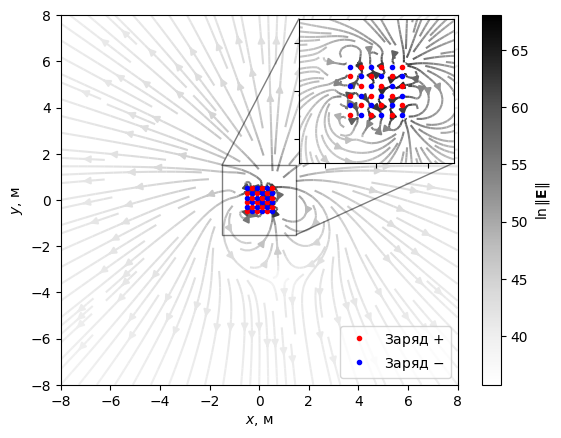
Построим поле 36 зарядов, расположенных равномерно в квадратной сетке \(6 \times 6\) при \(-0.5 \le x, y \le 0.5\). Число отрицательных и положительных зарядов одинаково - по 18 штук.

Для начала сформулируем функцию распределения точечных зарядов:

import numpy as np
from src.vectorfield import *


def create_charges(nq):
    vals = [-0.5 + i/(nq - 1) for i in range(nq)]
    qtopos = np.zeros((nq*nq, 3))
    for i, x in enumerate(vals):
        for j, y in enumerate(vals):
            count = j + nq*i + 1
            q = 1.02 * count if (i + j)%2 == 0 else -count
            qtopos[j + nq*i, :] = q, x, y
    return qtopos

…

from src.kahansum import *


def vecmag(rs):
    return np.sqrt(
        kahansum([r**2 for r in rs])
    )


def calc_potential(qtopos, rs):
    potvals = []
    for qri in qtopos:
        q, ri = qri[0], qri[1:]
        diffs = [r - ri for r in rs]
        dr = vecmag(diffs)
        potvals.append(q / dr)
    return kahansum(potvals)

…

qtopos = create_charges(6)
for y in 1., -1.:
    rs = [0., y]
    potval = calc_potential(qtopos, rs)
    print(rs, potval)

[0.0, 1.0] [ 9.09978832 14.55036178]
[0.0, -1.0] [ 4.48425367 -0.96631979]

Строим итоговую картину поля 36 зарядов:

qtopos = create_charges(6)
E = make_vector_field(qtopos)
mesh = create_mesh((-8, 8), (-8, 8), (150, 150))
field = E(mesh)
# График
color = np.log(field[0]**2 + field[1]**2)
fig, ax = plot_vectorfield_2d(
    mesh,
    field,
    color=color,
    cmap="Greys",
    density=1.5,
    cbar_label=r"$\ln{\| \mathbf{E} \|}$"
)
plot_charges(qtopos, (fig, ax))
axins = ax.inset_axes(
    [0.6, 0.6, 0.39, 0.39],
    xlim=(-1.5, 1.5), ylim=(-1.5, 1.5),
    xticklabels=[], yticklabels=[]
)
plot_vectorfield_2d(
    mesh,
    field,
    (fig, axins),
    color=color,
    cmap="Greys",
    density=5
)
plot_charges(qtopos, (fig, axins))
ax.indicate_inset_zoom(axins, edgecolor="k")
ax.set(xlabel="$x$, м", ylabel="$y$, м")
ax.legend();

mesh1 = create_mesh((-8, 8), (-8, 8), (150, 150))
mesh2 = create_mesh((-1.5, 1.5), (-1.5, 1.5), (150, 150))
field1 = E(mesh1)
field2 = E(mesh2)
# График
color = np.log(field1[0]**2 + field1[1]**2)
fig, (ax1, ax2) = plt.subplots(nrows=2, figsize=(10, 10))
plot_vectorfield_2d(
    mesh1,
    field1,
    (fig, ax1),
    color=color,
    cmap="Greys",
    cbar_label=r"$\ln{\| \mathbf{E}(x, y) \|}$",
    density=1.5
)
plot_charges(qtopos, (fig, ax1))
plot_vectorfield_2d(
    mesh2,
    field2,
    (fig, ax2),
    color=color,
    cmap="Greys",
    cbar_label=r"$\ln{\| \mathbf{E}(x, y) \|}$",
    density=1.5
)
plot_charges(qtopos, (fig, ax2))
ax1.set(xlabel="$x$, м", ylabel="$y$, м", aspect="equal")
ax2.set(xlabel="$x$, м", ylabel="$y$, м", aspect="equal")
ax1.legend();