Использование генераторов псевдослучайных чисел

Начнём рассмотрение вопроса с помощью стандартного модуля random. Абсолютно всю информацию о нём вы найдёте в официальной документации.

Основы

Импортируем модуль:

import random as rand

Сгенерируем 5 псевдослучайных чисел (ПСЧ):

for _ in range(5):
    print(rand.random())

0.4144996894808771
0.8148737509465089
0.9431492393399808
0.8417589859936887
0.49304928427331807

Функция random() генерирует ПСЧ, распределённое равномерно на полуотрезке [0, 1).

Note

Запустив этот код несколько раз, вы заметите, что каждый раз получаете различный результат. Ниже приведён тот же код, однако результат отличается.

for _ in range(5):
    print(rand.random())

0.9076672496198152
0.8524363746886503
0.28988182684694164
0.18949674376959746
0.30066679093127047

Состояние генератора

На самом деле в предыдущем примере мы вызвали не функцию random(), а метод random() экземпляра класса Random. Конкретный экземпляр класса Random имеет определённое состояние, которое по умолчанию случайно, но может определяется параметром seed (на русский часто переводится как “затравка”) или методом setstate(...) в любой момент работы программы.

Повторим предыдущий пример, задав определённое значение seed:

# Затравка может быть любым целым числом.
# Рекомендуют назначать его очень большим числом,
# чтобы уменьшить вероятность совпадения затравок,
# назначенных разными людьми
rand.seed(1700077)
for _ in range(5):
    print(rand.random())

0.7020746348844183
0.6233161107388304
0.12425768533206094
0.29613478392527026
0.5273751569843022

И ещё раз выполним этот же код:

rand.seed(1700077)
for _ in range(5):
    print(rand.random())

0.7020746348844183
0.6233161107388304
0.12425768533206094
0.29613478392527026
0.5273751569843022

Сколько бы раз мы не запустили код, мы будем получать одну и ту же последовательность значений. Таким образом наглядно показано свойство обеспечения воспроизводимости результатов ГПСЧ.

Изменим затравку - получим другой результат:

rand.seed(777)
for _ in range(5):
    print(rand.random())

0.22933408950153078
0.44559617334521107
0.36859824937216046
0.269835098321503
0.3361436466700177

Но теперь этот результат всё так же от запуска к запуску будет повторяться:

rand.seed(777)
for _ in range(5):
    print(rand.random())

0.22933408950153078
0.44559617334521107
0.36859824937216046
0.269835098321503
0.3361436466700177

Рассмотрим пример, показывающий неудобство использования метода seed() напрямую.

Пусть есть две функции, использующие внутри себя ГПСЧ, причём получают ПСЧ, распределённое по одинаковым законам. Пусть, например, функция f() генерирует ПСЧ, используя random(). То же делает и функция g():

def f():
    return rand.random()

def g():
    return rand.random()

Вызовем последовательно эти функции:

print(f(), g())

0.7523163560031157 0.9226950812763804

При каждом запуске получаем разные результаты. Но попробуем реализовать возможность воспроизведения результатов. Для этого вызовем seed(...) в глобальной области видимости:

rand.seed(666)
print(f(), g())

0.45611964897696833 0.9033231539802643

Мы добились своего - результат от запуска к запуску не меняется. Заметим ещё одно, а именно то, что результат не изменится, если мы поменяем местами вызовы функций:

rand.seed(666)
print(g(), f())

0.45611964897696833 0.9033231539802643

Note

Заметьте, в каждой ячейке мы должны вызвать seed(...), чтобы каждый раз переустанавливать ГПСЧ в начальное состояние. В противном случае будут генерироваться новые случайные числа, которые тем не менее всё так же воспроизводимы. Иными словами, если после вызова seed(...) мы сгенерировали \(m\) чисел, то при повторном запуске для генерации \(n\) чисел, \(n > m\), будут сгенерированы те же самые \(m\) чисел, плюс \(n - m\) новых чисел.

Убедимся в этом так. Опишем функцию генерации заданного количества ПСЧ:

def gen_randoms(n):
    return [
        rand.random() for _ in range(n)
    ]

И вызовем её для генерации сначала трёх, а затем двух чисел:

rand.seed(2023)
# Три случайных числа
print(gen_randoms(3))
# плюс два новых случайных числа
print(gen_randoms(2))

[0.3829219244542088, 0.9718620884907823, 0.8438174232038365]
[0.32028063842069, 0.5710257361341048]

А теперь сбросим ГПСЧ в то же самое начальное состояние и сгенерируем сразу пять чисел. В результате должна получиться та же самая последовательность ПСЧ:

rand.seed(2023)
print(gen_randoms(5))

[0.3829219244542088, 0.9718620884907823, 0.8438174232038365, 0.32028063842069, 0.5710257361341048]

Как видите, результат полностью предсказуем.

Note

Параметр seed(...) является глобальным. В программах, состоящих из нескольких модулей, это может стать проблемой.

В реальных программах со множеством модулей и большим объёмом кода рассмотренный подход имеет некоторые недостатки. В ряде задач, например, может потребоваться ГПСЧ, способный корректно работать в условиях параллельных вычислений. В условиях модульности программы может быть удобнее передавать между функциями и объектами экземпляры генератора.

Существует удобный способ справиться с описанными проблемами - создание экземпляра ГПСЧ определённого типа и с заданным состоянием. Например, так:

rg = rand.Random(2023)
# Переданный параметр по сути своей есть seed

Наш экзепляр ГПСЧ rg имеет все те же методы и возможности, что есть в модуле random, который мы использовали под псевдонимом rand. Перепишем нашу функцию gen_randoms(...) следующим образом:

def gen_randoms(n, rg):
    # Параметр rg - объект ГПСЧ
    return [
        rg.random() for _ in range(n)
    ]

Теперь, помимо количества генерируемых чисел, функция принимает на вход объект ГПСЧ rg. Сгенерируем пять чисел:

print(gen_randoms(5, rg))

[0.3829219244542088, 0.9718620884907823, 0.8438174232038365, 0.32028063842069, 0.5710257361341048]

Как видите, результат тот же, что и раньше при seed = 2023.

Визуализация распределений

Для визуализации случайных чисел часто используется гистограмма. Подключим matplotlib, сформируем два массива ПСЧ для двух разных распределений и построим их гистограммы. При формировании массивов воспользуемся методами normalvariate(...) (нормальное распределение) и uniform(...) (равномерное распределение) нашего экземпляра ГПСЧ rg.

import matplotlib.pyplot as plt

# Сформируем массивы по 50 элементов
N1 = 50
norm1 = [
    # mu - математическое ожидание
    # sigma - среднее квадратическое отклонение
    rg.normalvariate(mu=10, sigma=2)
    for _ in range(N1)
]
uniform1 = [
    rg.uniform(-1, 2)
    for _ in range(N1)
]

fig, (ax1, ax2) = plt.subplots(
    figsize=(6, 6), nrows=2
)
ax1.hist(norm1, bins=20)
ax1.set_title("Нормальное распределение")
ax2.hist(uniform1, bins=20)
ax2.set_title("Равномерное распределение");

Увеличим число точек в 20 раз:

N2 = N1 * 20
norm2 = [
    rg.normalvariate(mu=10, sigma=2)
    for _ in range(N2)
]
uniform2 = [
    rg.uniform(-1, 2)
    for _ in range(N2)
]

fig, (ax1, ax2) = plt.subplots(
    figsize=(6, 6), nrows=2
)
ax1.hist(norm2, bins=20)
ax1.set_title("Нормальное распределение")
ax2.hist(uniform2, bins=20)
ax2.set_title("Равномерное распределение");

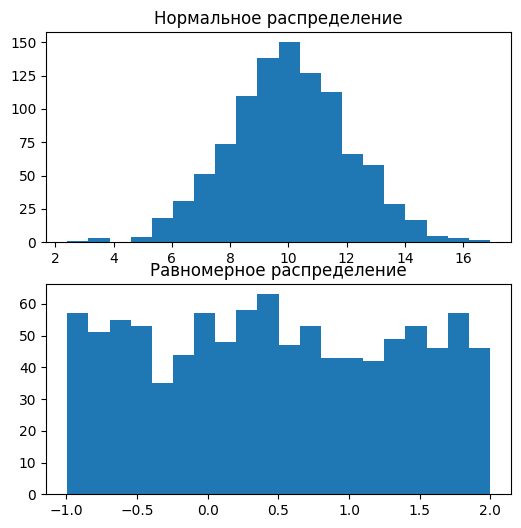
Как видите, при увеличении количества ПСЧ гистограммы принимают всё более чёткие очертания конкретного распределения.

Функциональность стандартного random уже достаточна для моделирования различных стохастических процессов. Однако в ряде случаев более удобно пользоваться random’ом из библиотеки NumPy.

Использование NumPy

Функционал numpy.random полностью аналогичен random’у стандартной библиотеки. Так как вся библиотека NumPy заточена под работу с массивами, методы numpy.random так же способны генерировать не одно число за раз, а сразу весь массив, матрицу или тензор заданного размера. И здесь также есть возможность пользоваться как неявно созданным экземпляром Generator, так и его явно созданным экземпляром. Создать генератор можно так:

import numpy.random as nprand

# Генератор по умолчанию с состоянием по затравке
rg = nprand.default_rng(seed=1234567)

Сразу сгенерируем два массива чисел, распределённых по нормальному и экспоненциальному законам:

fig, (ax1, ax2) = plt.subplots(nrows=2, figsize=(6, 8))
# density=True создаёт гистограмму плотности,
# по смыслу соответствующую функции плотности вероятности
# - нормальное
ax1.hist(
    rg.normal(loc=10, scale=2, size=10_000),
    bins=20,
    density=True
)
ax1.set(xlabel="$x$", ylabel=r"$p_{\mathrm{norm}}(x)$");
# - экспоненциальное
ax2.hist(
    rg.exponential(scale=3, size=10_000),
    bins=20,
    density=True
)
ax2.set(xlabel="$x$", ylabel=r"$p_{\exp}(x)$");

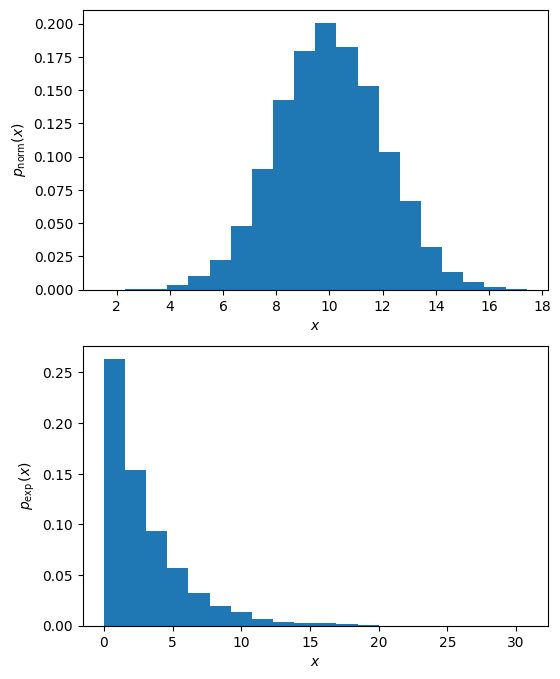
Мы сразу создали массив из 10000 элементов, указав параметр size=10000. Если size не указать, то будет возвращено одно число.

Note

Названия некоторых методов отличаются от тех же функций в стандартном random’ме. Отличаются и имена параметров функций. В данном случае параметры loc и scale аналогичны mu и sigma (математическое ожидание и стандартное отклонение).

fig, ax = plt.subplots()
x = rg.normal(10, 5, 10_000)
# Пусть y коррелирует с x
y = rg.normal(3, 2, 10_000) + x/3
img = ax.hist2d(x, y, bins=50, cmap="Greys", density=True)[-1]
fig.colorbar(img, ax=ax, label="$p(x, y)$")
ax.set(xlabel="$x$", ylabel="$y$");

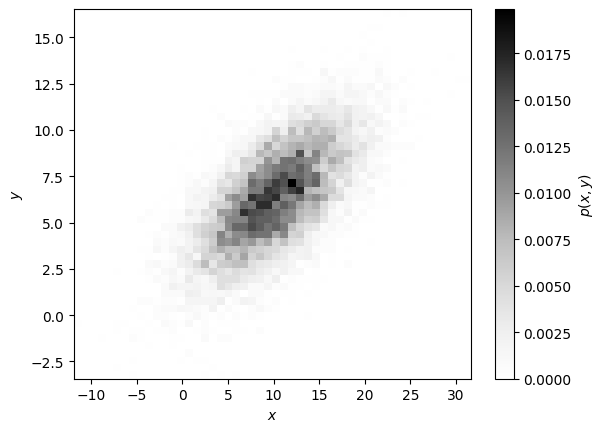
Случайную матрицу можно создать, передав в качестве size несколько значений:

# По умолчанию loc=0 и scale=1
rg.normal(size=(3, 4))

array([[ 0.83356875, -0.99563296, -1.49970249,  0.11628947],
       [ 0.36775022, -1.06158613, -0.27614625,  0.78144333],
       [ 1.0311598 , -0.64312952, -1.79305138,  1.42401372]])

Естественно, при одном и том же seed будет один и тот же результат и для чисел, и для массивов любой формы:

rg = nprand.default_rng(98765)
rg.exponential(size=(3, 4))

array([[0.02466916, 1.44229712, 0.96453594, 1.16304798],
       [0.22589411, 2.33248878, 1.33913539, 0.17395315],
       [0.73634616, 1.14181883, 1.27708772, 0.36814741]])

rg = nprand.default_rng(98765)
rg.exponential(size=(3, 4))

array([[0.02466916, 1.44229712, 0.96453594, 1.16304798],
       [0.22589411, 2.33248878, 1.33913539, 0.17395315],
       [0.73634616, 1.14181883, 1.27708772, 0.36814741]])

Одним из преимуществ numpy.random является возможность использования ГПСЧ в параллельных процессах. Эта возможность обеспечивается за счёт SeedSequence.

См. также

1. SeedSequence для применения ГПСЧ в параллельных вычислениях.

2. Основы генерации ПСЧ можно найти в учебнике “Имитационное моделирование”.

3. Книга “Python для сложных задач”.

4. Под визуализацию статистических данных заточена библиотека seaborn.

5. Документация numpy.random.

6. Генераторы NumPy основаны на низкоуровневых генераторах ПСЧ, которые называются Bit Generators. В документации на них можно найти полный список конкретных генераторов. Тогда вместо nprand.default_rng(...), создающего по умолчанию битовый генератор PCG64, можно, например, создать ГПСЧ с битовым генератором SFC64: nprand.Generator(nprand.SFC64()).

7. Документация стандартного random.