Поиск корней уравнений

Рассмотрим следующее трансцендентное уравнение:

\[\cos{x} = x.\]

Никак не получится преобразовать данное уравнение, чтобы точно определить значение \(x\). Поэтому решают его численно. Но перед численным решением всегда полезно оценить решение графически, ведь вполне может существовать несколько корней, в то время как численный метод находит только один корень. В таком случае важно понимать, какой именно корень найден численно. После этого появится понимание, как изменить параметры решателя так, чтобы он нашёл остальные корни в последующих поисках.

Графическое построение

import matplotlib.pyplot as plt
import numpy as np

# Исходные данные
# - массив значений аргумента 
# - и двух функций: cos(x) и x
x = np.linspace(-np.pi, np.pi, 300)
y_cos = np.cos(x)
y_x = x.copy()  # Копируем x, чтобы переменные x и y_x
                # не ссылались на одни и те же данные

# Заведём функцию построения графика f(x)
# и сможем строить его в любой момент
def plot_f():
    fig, ax = plt.subplots()
    ax.plot(x, y_cos, label=r"$\cos{x}$")
    ax.plot(x, y_x, label=r"$x$")
    ax.set(xlabel="$x$", ylabel="$y$", aspect="equal")
    ax.legend()
    # Вернём fig и ax, чтобы была возможность
    # достроить и/или изменить график
    return fig, ax

with plt.style.context("bmh"):
    fig, ax = plot_f()
    plt.show()

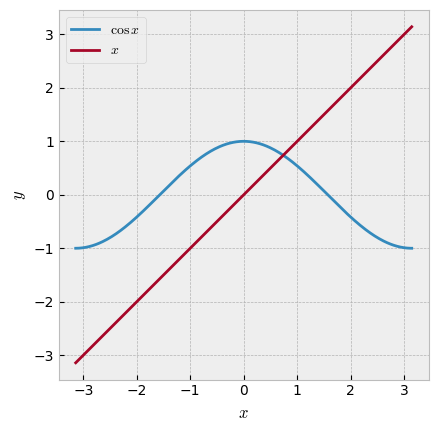
Итак, в данном случае существует единственный корень \(x_{\rm r}\), расположенный где-то между \(0.5\) и \(1\): \(x_{\rm r} \in (0.5; 1)\).

Численный поиск корня

Найти корень уравнения \(\cos{x} = x\) значит найти такое значение \(x_{\rm r}\), при котором значение функции

\[f(x) = \cos{x} - x\]

равно \(0\): \(f(x_{\rm r}) = 0\).

Рассматриваемая функция \(f(x)\) является скалярной, т. к. отображает скалярный аргумент \(x \in \mathbb{R}\) в скалярное значение \(y = f(x) \in \mathbb{R}\). Помимо скалярных существуют векторные функции, зависящие от нескольких аргументов \(x_1, x_2, \ldots\), собранных в вектор входных параметров \(\mathbf{x}\), однако значение самой функции является скалярной величиной: \(f: \mathbf{x} \rightarrow y\).

Опишем рассмотренную скалярную функцию \(f(x)\) в коде:

def f(x):
    return np.cos(x) - x

Функции численного поиска корней содержатся в модуле optimize библиотеки SciPy. То, что указанный модуль называется “оптимизацией”, не должно вводить в заблуждение. Дело в том, что численный поиск корней уравнений во многом схож с методами численного поиска экстремумов (минимумов, оптимумов) функций.

Для текущей цели понадобится алгоритм поиска корня скалярной функции root_scalar(...). Импортируем:

from scipy.optimize import root_scalar

Найдём корень. Для этого нужно вызвать функцию root_scalar(...) с необходимыми аргументами. Первым аргументом передаётся имя целевой функции: в нашем случае f. Далее необходимо задать метод поиска корня уравнения. Их существует большое множество, и все они подробно описаны в документации SciPy - выбор за программистом.

Выбрать метод можно явно, задав параметр method="newton" (например, метод Ньютона), или неявно. Например, ниже задаётся интервал оси \(Ox\), на котором предполагается нахождение корня. В этом случае, если явно не указан метод, он будет назначен автоматически (в данном случае используется метод "brentq"):

res = root_scalar(f, bracket=(0.5, 1.))

Посмотрим, какая информация содержится в результате res:

res

      converged: True
           flag: converged
 function_calls: 7
     iterations: 6
           root: 0.7390851332151607
         method: brentq

Информация следующая:

• converged: True и flag: converged - корень успешно найден, решение сошлось;

• function_calls: 8 - целевая функция f была вызвана 8 раз;

• iterations: 7 - алгоритм поиска завершился за 7 итераций;

• root: 0.7390851332151606 - искомый корень.

Служебная информация (всё, кроме root) позволяет оценивать эффективность использованного алгоритма. За чем меньшее число итераций выполняется алгоритм, чем меньше раз вызывается целевая функция - тем быстрее выполняется алгоритм.

Сохраним гайденный корень в отдельной переменной:

root = res.root
root

0.7390851332151607

Перестроим график и отметим на нём найденное решение. Функции plot(...) передадим root в качестве аргумента x, а в качестве аргумента y можно передать либо np.cos(root), либо просто root, т. е. нужно подставить root в любую из двух частей уравнения:

with plt.style.context("bmh"):
    fig, ax = plot_f()
    ax.plot(
        root, root,
        ls="", marker="o", label="Корень"
    )
    plt.show()

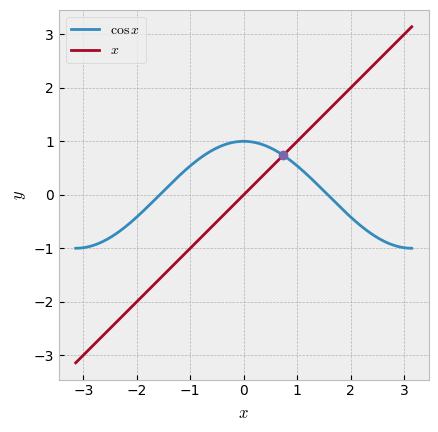
Действительно, найдено верное решение уравнения.

Мы рассматриваем очень простое трансцендентное уравнение \(\cos{x} = x\). Простое оно потому, что имеет единственный корень и рассчитывается довольно быстро. В учебном процессе встречаются более сложные уравнения, для поиска корней которых требуется грамотно выбрать метод численного решения. Ниже приведён пример решения того же уравнения методом Ньютона.

Поиск корня другим методом

Найдём корень методом Ньютона (залючим вызов root_scalar(...) в блок try...except, т. к. первые попытки будут приводить в ошибкам):

try:
    res = root_scalar(f, method="newton")
except Exception as ex:
    # Перехватили исключение,
    # чтобы не рушить интерпретатор
    print(ex)

x0 must not be None for newton

В возникшем исключении содержится сообщение, что для метода newton необходимо задать x0 - начальное значение аргумента. Сделаем это, учтя, что корень расположен вблизи \(x = 0.5\):

res = root_scalar(f, method="newton", x0=0.5)
res

      converged: True
           flag: converged
 function_calls: 8
     iterations: 4
           root: 0.7390851332151606
         method: newton

Получили то же значение \(x_{\rm r}\), что и предыдущим методом brentq. Посмотрим, изменятся ли параметры решения (число вызовов функции и итераций алгоритма), если изменится начальное приближение x0:

# Пусть x0 выбрано очень не удачно,
# т. е. вдали от решения
res = root_scalar(
    f, method="newton", x0=-3
)
res

      converged: False
           flag: convergence error
 function_calls: 100
     iterations: 50
           root: -422.1067876274537
         method: newton

Как видно, количество function_calls и iterations возросло более чем в 6 раз. Будь на месте \(f(x)\) более сложная функция, одно вычисление которой занимало бы 1 минуту, то суммарное время поиска корня увеличилось бы с 8 мин. до 52 мин.

Метод Ньютона использует знание о производных функции. Если производная не задана методу явно, то её вычисление производится численно “под капотом”. Мы можем попробовать исправить возникшую ситуацию, явно передав производную f в функцию root_scalar(...). Производная \(f(x)\) имеет вид:

\[f'(x) = -\sin{x} - 1.\]

def f_der(x):
    return -np.sin(x) - 1

res = root_scalar(f, method="newton", x0=-3, fprime=f_der)
res

      converged: False
           flag: convergence error
 function_calls: 100
     iterations: 50
           root: 1.1641729138555427e+17
         method: newton

Катастрофа! Мало того, что число вызовов функции увеличилось на порядок, так ещё и корень не найден! Так бывает довольно часто. Мы смогли построить уравнение графически, оценив значение корня. На практике может случиться так, что и построение графика затруднительно. Представьте, что вам нужно решать сложное уравнение 1000 раз при различных значениях параметров, из-за чего корень каждый раз будет в новых пределах. И каждый из 1000 раз вам нужно вручную оценивать значение корня. Сколько времени это займёт? Очевидно, достаточно, чтобы провести за этим занятием лучшие годы жизни. Нужно уметь решать уравнения численно в общем виде.

В данном случае проблема применения метода Ньютона обусловлена периодичностью функции \(\cos{x}\) - части целевой функции \(f(x)\). График \(f(x)\) показан ниже:

# Для наглядности возьмём диапазон x побольше
x = np.linspace(-10, 10, 500)

with plt.style.context("bmh"):
    fig, ax = plt.subplots()
    ax.plot(x, np.cos(x) - x)
    ax.set(xlabel="$x$", ylabel="$f(x)$", aspect="equal")
    plt.show()

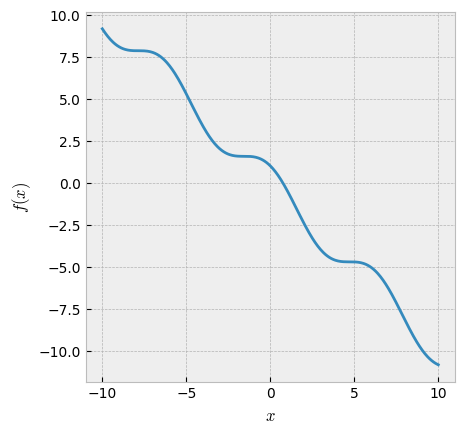
Периодичность уравнения может приводить к появлению локальных минимумов (вот и связь с оптимизацией) или точек перегиба функции \(f(x)\), из которых метод Ньютона выбраться не способен, т. к. теряет информацию о поведении целевой функции из-за обнуления её производных в таких точках. Неудачная точка x0=-3 неудачна как раз из-за того, что находится очень близко к точке перегиба \(f(x)\).

А как поведёт себя метод brentq в случае задания очень широкого диапазона поиска? Посмотрим:

res = root_scalar(f, method="brentq", bracket=(-100, 100))
res

      converged: True
           flag: converged
 function_calls: 9
     iterations: 8
           root: 0.7390851332151586
         method: brentq

Метод Брента отлично справляется с задачай, причём число вызовов целевой функции почти не изменилось! Не зря данный метод считается одним из самых надёжных в библиотеке SciPy.

Attention

Заметьте, что значение root немного отличается от найденного этим же методом ранее. Численные методы никогда не дают абсолютно точный результат при различных исходных данных!

Таким образом, при численном поиске корней уравнения необходимо понимать сильные и слабые стороны методов поиска, а также помнить о возможности наличия нескольких корней уравнения и о возможном появлении локальных минимумов целевой функции \(f(x)\). К численному решению уравнений (в том числе и дифференциальных) требуется подходить с умом (как и ко всему в этом мире).

Таковы основы численного поиска корней уравнений. Больше информации вы найдёте в официальной документации используемых вами библиотек.