Решение обыкновенных дифференциальных уравнений (ОДУ)#
Решатели ОДУ и их систем содержатся в пакете scipy.integrate.
Стандартные функции решают ОДУ вида
где в левой части стоит первая производная \(\dot{y} = \mathrm{d}y / \mathrm{d} t\) искомой функции \(y\), зависящая в общем случае от независимого аргумента \(t\) (это не обязательно время) и самой искомой функции \(y\). Правая часть ОДУ \(f\) в общем случае также зависит от \(t\) и \(y\).
В плане алгоритма решения ничего не изменится, если \(t\) и \(y\) будут векторами. Тогда ОДУ первого порядка (2) превратится в систему ОДУ первого порядка.
С точки зрения программирования требуется описать лишь правую часть уравнения (или системы) (2).
Задача#
В качестве примера рассмотрим задачу построения траектории движения тела, брошенного под углом к горизонту, с учётом сопротивления воздуха. Данная задача аналитически без серьёзных допущений не решается.
Математическая модель#
Пусть шар массой \(m\) брошен под углом \(\alpha\) к горизонту из начала координат системы \(Oxy\). Коэффициент лобового сопротивления шара \(c_{\rm drag}\).
Динамика полёта шара описывается векторным уравнением вида (2-ой закон Ньютона)
где \(\vec{v}\) и \(v\) - вектор скорости шара и её абсолютное значение соответственно; \(\rho\) - плотность воздуха; \(S\) - площадь сечения (миделя); \(\vec{g}\) - вектор ускорения свободного падения. Знак “\(-\)” соответствует тому факту, что вектор силы лобового сопротивления противоположно направлен вектору скорости. Направление вектора скорости задаётся единичным вектором \(\vec{v} / v\).
Сократим \(v\) в числителе и знаменателе и разделим обе части уравнения на \(m\):
Как известно, скорость - это производная координаты по времени: \(\vec v = \vec{\dot r}\). Здесь \(\vec r = (x, y)^\mathrm{T}\) - радиус-вектор материальной точки (шара).
Note
Транспонирование означает лишь то, что мы работаем с векторами-столбцами. Транспонировать векторы в коде не нужно.
Теперь наше ОДУ записывается так:
Получили ОДУ второго порядка.
Часто используемые методы численного интегрирования не работают с векторными уравнениями и способны решать только ОДУ первого порядка. Поэтому для численного интегрирования нам необходимо, во-первых, уйти от векторной формы записи ОДУ к скалярной и, во-вторых, свести уравнение второго порядка к системе уравнений первого порядка.
Запишем нашу систему в проекциях на оси СК, уйдя от векторной формы:
Получили систему ОДУ 2-го порядка. Теперь понизим порядок, учитывая, что \(\dot x = v_x\) и \(\dot y = v_y\):
Готово. Получена система ОДУ первого порядка: в левых частях стоят только первые производные, а в правых - производные отсутствуют.
Note
Обратите внимание, что \(v\) - это абсолютное значение вектора скорости \(\vec v\), а \(v_x\) и \(v_y\) - значения составляющих этого вектора по осям \(Oxy\), т.е. проекции на эти оси: \(v = \|\vec v\| = \sqrt{v_x^2 + v_y^2}\).
Пусть система координат (СК) \(Oxy\) имеет горизонтальную ось \(Ox\), направленную вправо, и вертикальну ось \(Oy\), направленную вверх. Тогда \(\vec{g} = (0, -9.81)^\mathrm{T}\) м/с\(^2\).
Для интегрирования необходимо задать начальные условия. В данном случае это координаты и проекции скорости шара в начальный момент времени \(t_0 = 0\). Начальные координаты зададим напрямую: \(x(0) = x_0\) и \(y(0) = y_0\). Вектор начальной скорости зададим через абсолютное значение \(v_0 = v(0)\) и угол бросания \(\alpha\): \(v_{x0} = v_0 \cos{\alpha}\) и \(v_{y0} = v_0 \sin{\alpha}\).
Интегрируя уравнения (3) при заданных начальных условиях, получим зависимости \(v_x(t)\), \(v_y(t)\), \(x(t)\) и \(y(t)\). Траектория будет построена по массивам значений \(x(t)\) и \(y(t)\).
Программная реализация#
# 100% понадобится NumPy
import numpy as np
Проекция на вертикаль вектора ускорения свободного падения \(g_y = -9.81\) м/с\(^2\):
FREE_FALL = -9.81
Систему (3) опишем в функции ode_sys(t, y...):
def ode_sys(t, y, c_drag, air_dense, m, s_mid):
# y[0] = v_x
# y[1] = v_y
# y[2] = x
# y[3] = y
# Абсолютная скорость
v = np.sqrt(y[0]**2 + y[1]**2)
# Вспомогательная переменная,
# чтобы не считать одно и то же два раза
coeff = 0.5 * c_drag * s_mid * air_dense * v / m
return (
-coeff * y[0], # dv_x / dt
-coeff * y[1] + FREE_FALL, # dv_y / dt
y[0], # dx / dt
y[1] # dy / dt
)
Первые два аргумента - время t и вектор значений переменных в этот момент y - обязательны и идут именно в таком порядке.
Последующие аргументы являются дополнительными.
Начальные условия. Пусть \(x_0 = 0\), \(y_0 = 0\), \(v_0 = 50\) м/с и \(\alpha = 57.3^\circ\), откуда рассчитаем \(v_{x0}\) и \(v_{y0}\):
x0, y0 = 0., 0.
v0 = 50.
alpha = np.radians(53.7)
v_x0 = v0 * np.cos(alpha)
v_y0 = v0 * np.sin(alpha)
# Итоговый массив начальных условий
# в порядке записи уравнений для решателя
# (см. функцию ode_sys)
y0 = [v_x0, v_y0, x0, y0]
Также зададим остальные параметры задачи:
rho = 1.25 # Плотность воздуха, кг/м^3
c_drag = 1. # Коэф-т лоб. сопротивления
m = 0.5 # Масса шара, кг
d = 0.1 # Диаметр шара, м
# Площадь миделя, м^2
S = 0.25 * np.pi * d**2
Интегрируем:
# Импортируем функцию решения задачи Коши
# (IVP - Initial Value Problem и есть задача Коши)
from scipy.integrate import solve_ivp
t_span = 0., 8.
sol = solve_ivp(
ode_sys,
t_span,
y0,
args=(c_drag, rho, m, S),
dense_output=True
)
print(sol)
message: The solver successfully reached the end of the integration interval.
success: True
status: 0
t: [ 0.000e+00 2.828e-05 3.111e-04 3.139e-03 3.142e-02
3.143e-01 1.170e+00 2.502e+00 4.737e+00 6.903e+00
8.000e+00]
y: [[ 2.960e+01 2.960e+01 ... 6.333e+00 4.664e+00]
[ 4.030e+01 4.030e+01 ... -2.667e+01 -2.889e+01]
[ 0.000e+00 8.372e-04 ... 9.737e+01 1.034e+02]
[ 0.000e+00 1.140e-03 ... -2.441e+01 -5.499e+01]]
sol: <scipy.integrate._ivp.common.OdeSolution object at 0x00000199D8E26470>
t_events: None
y_events: None
nfev: 68
njev: 0
nlu: 0
Как видим функция solve_ivp(...) принимает на вход функцию, в которой описано ОДУ или система ОДУ, интервал интегрирования t_span, вектор начальных условий y0.
Поскольку наша ode_sys принимает дополнительные параметры, то мы перечисляем их в том же порядке в списке args.
Аргумент dense_output необходим для того, чтобы в экземпляре решения sol решатель сохранил функции интерполяции \(v_x(t)\), \(v_y(t)\), \(x(t)\) и \(y(t)\).
Тогда мы сможем получить вектор y в любой момент времени t в пределах t_span следующим образом: sol.sol(t).
Note
По умолчанию dense_output = False и экземпляр решения (в данном случае sol) не имеет поля sol, т.е. sol.sol(t) вызовет ошибку.
Из результата следует, что в переменной sol содержатся массивы t и y, хранящие моменты времени и вектор значений интегрированных значений в эти моменты, а также др. служебную информацию.
Например, nfenv - число вызовов функции ode_sys.
Обратите внимание на то, что в выводе присутствует поле sol, имеющее тип OdeSolution - это и есть функция интерполяции решения, сохранённая благодаря dense_output = True.
Построим графики полученного решения:
import matplotlib.pyplot as plt
# Разобьём интервал времени на любое число точек
t = np.linspace(*t_span, 300)
# Получим интерполированные значения для t
res = sol.sol(t)
# Распакуем результат по отдельным массивам
vx, vy = res[0], res[1]
x, y = res[2], res[3]
# Строим четыре графика
fig, ((ax_vx, ax_vy), (ax_x, ax_y)) = \
plt.subplots(2, 2, figsize=(6, 8))
ax_vx.plot(t, vx)
# Расчётные точки
ax_vx.plot(sol.t, sol.y[0], ls="", c="orange", marker=".")
ax_vx.set(xlabel="$t$, сек", ylabel="$v_x$, м/с")
ax_x.plot(t, x)
# Расчётные точки
ax_x.plot(sol.t, sol.y[2], ls="", c="orange", marker=".")
ax_x.set(xlabel="$t$, сек", ylabel="$x$, м")
ax_vy.plot(t, vy)
# Расчётные точки
ax_vy.plot(sol.t, sol.y[1], ls="", c="orange", marker=".")
ax_vy.set(xlabel="$t$, сек", ylabel="$v_y$, м/с")
ax_y.plot(t, y)
# Расчётные точки
ax_y.plot(sol.t, sol.y[3], ls="", c="orange", marker=".")
ax_y.set(xlabel="$t$, сек", ylabel="$y$, м");
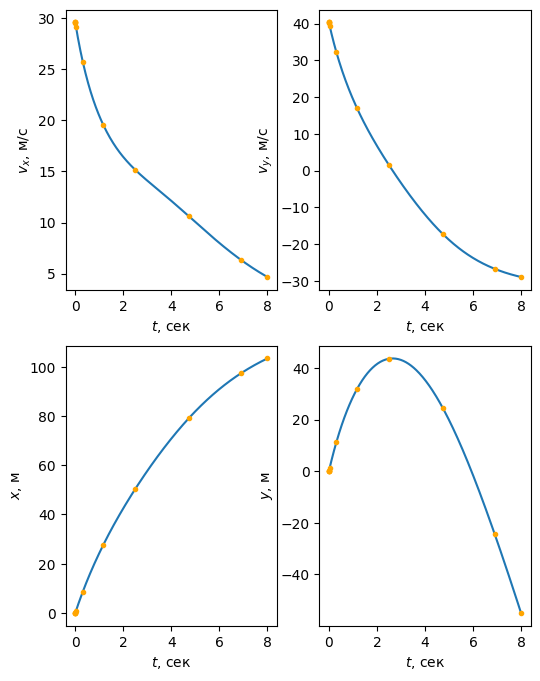
Траектория полёта:
fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(sol.y[2], sol.y[3], c="orange", ls="", marker=".")
ax.axhline(0, ls="-.", c="k")
ax.set(xlabel="$x$, м", ylabel="$y$, м", aspect="equal");
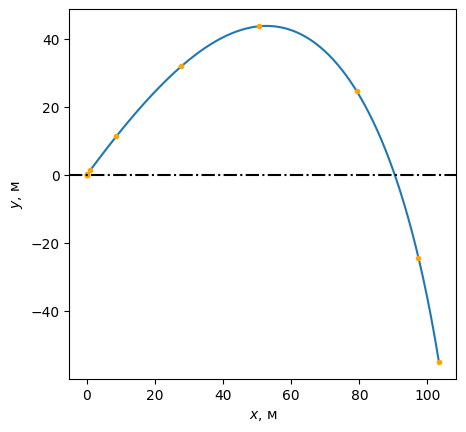
Интервал времени велик, вследствие чего шар “проваливается” сквозь поверхность \(y = 0\).
В SciPy предусмотрена возможность прерывания решения по заданному условию.
Для этого используется параметр event функции solve_ivp, посредством которого передаётся функция-условие, которую мы должны описать.
Функция-условие падения шара на землю (\(y = 0\)) описана ниже.
Она обязана принимать все те же параметры, что и функция системы ОДУ ode_sys.
# Поскольку здесь нам не нужны доп. аргументы
# c_drag, air_dense, m и s_mid, то мы просто используем
# синтаксис произвольного числа аргументов *args
def ev_fallen(t, y, *args):
# Считается, что событие наступает тогда,
# когда данная функция возвращает 0
return y[3] # y-координата
# Можно было бы написать и так:
# return y[3] - 0
# но это, очевидно, то же самое.
# Тем не менее, вместо 0 мы можем написать 10,
# и тогда событие наступит, когда шар будет
# снизится до высоты 10 м.
# Далее укажем следующее:
# - при выполнении условия решение должно прерваться:
ev_fallen.terminal = True
# - направление изменения координаты -1:
# с положительного на отрицательное
ev_fallen.direction = -1
Свойство направления перехода через значение direction позволяет обходить проблему, связанную с тем, что \(y(0)\) у нас тоже равна \(0\). Без указания направление прохода через \(0\) решение прервалось бы в самом начале.
Снова проинтегрируем при том же t_span, но с условием ev_fallen:
sol = solve_ivp(
ode_sys,
t_span,
y0,
args=(c_drag, rho, m, S),
dense_output=True,
# Вот наше условие прерывания
events=ev_fallen
)
print(sol)
message: A termination event occurred.
success: True
status: 1
t: [ 0.000e+00 2.828e-05 3.111e-04 3.139e-03 3.142e-02
3.143e-01 1.170e+00 2.502e+00 4.737e+00 5.935e+00]
y: [[ 2.960e+01 2.960e+01 ... 1.060e+01 8.125e+00]
[ 4.030e+01 4.030e+01 ... -1.718e+01 -2.345e+01]
[ 0.000e+00 8.372e-04 ... 7.920e+01 9.038e+01]
[ 0.000e+00 1.140e-03 ... 2.458e+01 3.553e-15]]
sol: <scipy.integrate._ivp.common.OdeSolution object at 0x00000199DBFEA080>
t_events: [array([ 5.935e+00])]
y_events: [array([[ 8.125e+00, -2.345e+01, 9.038e+01, 3.553e-15]])]
nfev: 62
njev: 0
nlu: 0
Изменился статус решения - оно было прервано событием.
Кроме того, появилось ещё два поля: t_events и y_events, хранящие момент времени наступления события и вектор решения в этот момент.
Теперь посмотрим на траекторию:
# Теперь при формировании массива t используем
# время наступления события падения шара на поверхность
# (приходится использовать два индекса из-за того,
# как решатель сохраняет t_events)
t = np.linspace(t_span[0], sol.t_events[-1][0])
res = sol.sol(t)
x, y = res[2], res[3]
fig, ax = plt.subplots()
ax.plot(x, y)
# Покажем точки решения
ax.plot(sol.y[2], sol.y[3], c="orange", ls="", marker=".")
ax.axhline(0, ls="-.", c="k")
ax.set(xlabel="$x$, м", ylabel="$y$, м", aspect="equal");
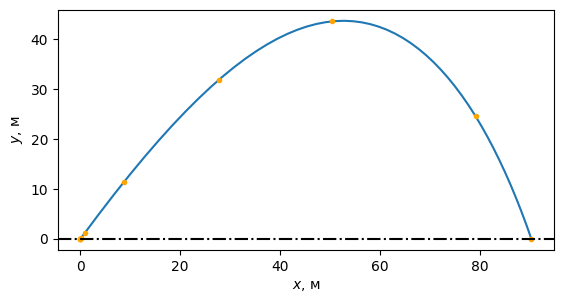
Если для события terminal = False (по умолчанию это так), то после его наступления решение продолжится до конца интервала интегрирования.
По умолчанию direction = 0, что соответствует переходу значения в любом направлении (с \(+\) на \(-\) или с \(-\) на \(+\)).
Функции-условия могут иметь сколь угодно сложный вид.
Заключение#
Функции решения систем ОДУ содержатся в модуле
scipy.integrate.Для численного интегрирования системы ОДУ необходимо привести её к первому порядку в скалярном виде.
Необходимо задать начальные условия для решения задачи Коши и интервал интегрирования
t_spanв том же порядке, что описан в функции, реализующей систему ОДУ.Параметр
dense_outputотвечает за сохранение в функций, интерполирующих результаты решения.Функции, переданные через
events, позволяют сохранять метки времениt_eventsи решения в эти моментыy_eventsпри заданных условиях. При необходимости можно прерывать интегрирование при наступлении событий. Сигнатуры функции, описывающей систему ОДУ, и функции-события должны совпадать.
См. также#
solve_ivp(...)имеет параметрmethod, через который можно задать метод интегрирования, коих существует множество. По умолчанию используется метод Рунге-Кутты четвёртого-пятого порядка (RK45).Метод LSODA подходит для решения жёстких систем ОДУ.
Для решения краевых задач имеется функция
solve_bvp(...)(BVP - Boundary Value Problem).
